
- •Жидкость и ее свойства.
- •2.Коэффициенты сжимаемости.
- •Закон Ньютона о внутреннем трении жидкости.
- •Коэффициенты вязкости. Условная вязкость.
- •Вискозиметр Энглера
- •Силы, действующие в жидкости.
- •Давление в точке покоящейся жидкости.
- •Свойства давления в точке покоящейся жидкости.
- •Дифференциальные уравнения равновесия жидкости в двух формах.
- •Относительный покой жидкости.
- •Основное уравнение гидростатики.
- •13.Манометрическое и вакуумное давление.
- •14. Сообщающиеся сосуды
- •15. Сила давления жидкости на плоскую стенку
- •Центр давления
- •С ила давления жидкости на криволинейную стенку.
- •Тело давления
- •Закон Архимеда
- •Методы описания движения
- •Виды движения
- •Элементы струйной модели
- •Потоки и их виды
- •Гидравлические элементы потока.
- •28. Дифференциальное уравнение движения идеальной жидкости
- •3.2. Уравнение Бернулли для идеальной жидкости
- •35.Уравнение Бернулли для элементарной струйки реальной жидкости
- •3.3. Уравнение Бернулли для реальной жидкости
- •37. Коэффициент Кориолиса
- •38. Мощность потока
- •39. Практическое применение уравнения Бернулли
- •40. Потери напора по длине
- •41. Потери напора в местных сопротивлениях
- •42. Режимы движения жидкости.
- •43. Опыт Рейнольдса
- •44. Коэффициент Дарси
- •Формула Дарси — Вейсбаха
- •[Править] Определение коэффициента потерь на трение по длине
- •[Править] Определение коэффициента Дарси для местных сопротивлений
- •45. Местные сопротивления
- •46. Расчет простого трубопровода
- •47. Истечение жидкости через насадки
- •48. Истечение жидкости через малые отверстия
- •49. Параллельное соединение трубопроводов
- •50. Последовательное сопротивление трубопроводов.
38. Мощность потока
Удельная энергия представляет работу, которую может выполнить единица массы, объема или веса жидкости, а мощность равна работе в единицу времени всей массы, объема или веса. Поэтому для получения мощности необходимо полные напоры умножить соответственно на расходы: массовый Qm=ρQ, объемный Q или весовой ρgQ. В результате этого получим
Nп=eпρQ=ρпQ=HρgQ.
Единица измерения в системе СИ – Н*м/с=Дж/с=Вт
Приращение мощности, получаемое потоками, проходящими через гидравлические и пневматические машины, определяется по перепаду полных удельных энергий входящего eп1 и выходящего eп2 потоков из машины: еп=еп2-еп1, соответственно рп=рп2-рп1; Н=Н2-Н1.
39. Практическое применение уравнения Бернулли
В телефоне
40. Потери напора по длине
Потери
напора по длине, иначе их называют
потерями напора на трение
![]() ,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью
,
в чистом виде, т.е. так, что нет никаких
других потерь, возникают в гладких
прямых трубах с постоянным сечением
при равномерном течении. Такие потери
обусловлены внутренним трением в
жидкости и поэтому происходят и в
шероховатых трубах, и в гладких. Величина
этих потерь выражается зависимостью
![]() ,
,
где
![]() -
коэффициент сопротивления, обусловленный
трением по длине.
-
коэффициент сопротивления, обусловленный
трением по длине.
При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы
![]() ,
,
где l– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).
Из этого выражения нетрудно видеть, что значение l - коэффициент трения участка круглой трубы, длина которого равна её диаметру.
С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси
![]() .
.
Эту
формулу можно применять не только для
цилиндрических трубопроводов, но тогда
надо выразить диаметр трубопровода d
через гидравлический
радиус потока
![]()
![]() или
или
![]() где,
напомним, Й
– площадь живого сечения потока,
где,
напомним, Й
– площадь живого сечения потока,
З - смоченный периметр.
Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид
![]() .
.
Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине »не является величиной постоянной.
Д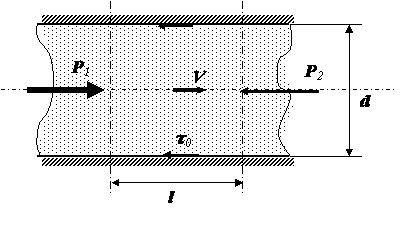 ля
определения физического смысла
коэффициента »рассмотрим
объём жидкости длиной l,
который равномерно движется в трубе
диаметром d
со скоростью V.
На этот объём действуют силы давления
P1
и P2,
причём P1>
P2,
и силы трения рассматриваемого объёма
о стенки трубы, которые определяются
напряжением трения на стенке трубы Д0.
Условием равномерного движения под
действием сказанных сил будет следующее
равенство:
ля
определения физического смысла
коэффициента »рассмотрим
объём жидкости длиной l,
который равномерно движется в трубе
диаметром d
со скоростью V.
На этот объём действуют силы давления
P1
и P2,
причём P1>
P2,
и силы трения рассматриваемого объёма
о стенки трубы, которые определяются
напряжением трения на стенке трубы Д0.
Условием равномерного движения под
действием сказанных сил будет следующее
равенство:
![]() .
.
Если учесть, что
![]() ,
то
,
то
![]() ,
,
и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:
![]() .
.
Сократив
последнее выражение, получим
![]() .
Выразив из него »,
окончательно будем иметь
.
Выразив из него »,
окончательно будем иметь
 .
.
Из полученного выражения следует, что коэффициент гидравлического трения есть величина, пропорциональная отношению напряжения трения на стенке трубы к гидродинамическому давлению, посчитанному по средней скорости потока. Приведённые выше рассуждения и полученные в результате них формулы справедливы как для ламинарного, так и для турбулентного потоков. Однако коэффициент »не является величиной постоянной и зависит от многих факторов. Для выяснения его величины, и связанных с ним потерь энергии необходимо подробно проанализировать режимы движения жидкости.
