35.Уравнение Бернулли для элементарной струйки реальной жидкости

3.3. Уравнение Бернулли для реальной жидкости

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

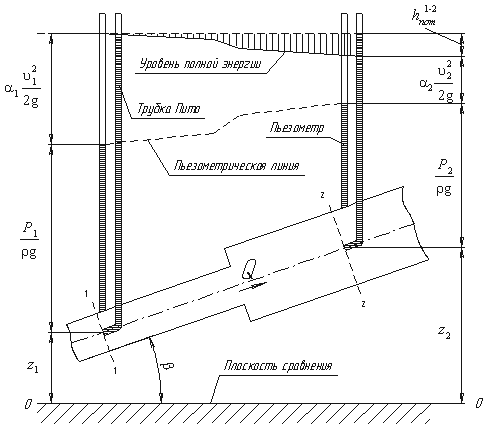
Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

= h_лин + h_мест

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ₁ω ₁ = υ₂ω₂.

37. Коэффициент Кориолиса

Коэффициент Кориолиса. Для применения уравнения Бернулли необходимо знать величину удельной энергии[14, С.60] Коэффициент Кориолиса, представляющий собой отношение действительной кинетической энергии к кинетической энергии, вычисленной при условии движения всех частиц в сечении с одной и той же скоростью, равной средней скорости, может быть найден следующим образом.[256, С.43] Коэффициент Кориолиса при турбулентном режиме течения меняется в пределах от 1,11 до 1,15. Большие значения коэффициента Кориолиса соответствуют меньшим, числам Рейнольдса .[7, С.22] Коэффициент Кориолиса k — есть функция от числа Рейнольдса и геометрических характеристик горловины_(отнссительной толщины ее кромок).[212, С.129] Коэффициент Кориолиса а является определенной величиной и характеризует степень неравномерности распределения скоростей по живому сечению потока. Установлено, что а> I и обычно его значение заключено в пределах а =1,03-=- 1,1. В инженерной практике чаще всего принимают а=1. В некоторых случаях, например, при явно ламинарном режиме движения жидкости в[294, С.52] Обычно коэффициент Кориолиса определяется опытным путем. Он зависит от степени неравномерности распределения скоростей в поперечном сечении потока и всегда больше единицы; для так называемого ламинарного режима (см. стр. 115) в цилиндрической трубе а = 2, а для так называемого турбулентного режима а = = 1,0454-1,10.[221, С.78] Однако коэффициент Кориолиса следует учитывать лишь при ламинарном режиме течения, когда а = 2. Для турбулентных потоков можно принимать а=1.[201, С.33]