31)Энтропия. Второе начало термодинамики.

Энтропия – это количественная характеристика беспорядка в системе.

Второе начало термодинамики:

1.Любой необратимый процесс в замкнутой системе происходит так, что энтропия возрастает.

2.Невозможен круговой процесс, в котором теплота от менее нагретого тела передаётся более нагретому телу.

32. * Вывод основного уравнения молекулярно-кинетической теории газов***(убейтесь сразу, если попадётся на экзамене)(слямзено с википедии, так что, если что упустил, проверьте)

Пусть имеется кубический сосуд с ребром длиной   и одна частица массой   в нём.

Обозначим скорость движения  , тогда перед столкновением со стенкой сосуда импульс частицы равен , , а после —  , поэтому стенке передается импульс  . Время, через которое частица сталкивается с одной и той же стенкой, равно 

.

Отсюда следует:

,

Так как давление  ,, следовательно сила 

Подставив, получим: ,

Преобразовав: ,

Так как рассматривается кубический сосуд, то 

Отсюда:

.

Соответственно ,  и  .

Таким образом, для большого числа частиц верно следующее: . , аналогично для осей y и z.

Поскольку , , то , . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.

Отсюда ,

или  .

Пусть ,  — среднее значение кинетической энергии всех молекул, тогда:

, , откуда , .

Для одного моля выражение примет вид ,

33. Максвелловское распределение молекул по скоростям. Наиболее вероятная скорость. Зш распределения энергии по степеням свободы.

Закон распределения молекул по скоростям Максвелла описывает стационарное распределение молекул однородного одноатомного идеального газа по скоростям в условиях термодинамического равновесия и отсутствия внешнего силового поля. Максвелловское распределение молекул по скоростям устанавливается в результате взаимных столкновений между молекулами при их хаотическом тепловом движении. Если в соответствующей формуле заменить скорость молекулы на ее кинетическую энергию, тогда мы вместо распределения по скоростям получим распределение по энергиям. 

Наиболее вероятная скорость, ,  — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению , . Чтобы найти её, необходимо вычислить  , приравнять её нулю и решить относительно , :

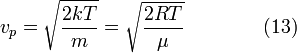
Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия. Поступательное движение молекул характеризуется средней кинетической энергией, равной ,  . Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия

В однородном газе, молекулы которого имеют любое число степеней свободы i, каждая молекула в среднем обладает энергией движения, равной

34)Распределение Больцмана. Барометрическая формула.

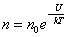– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

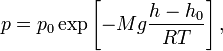барометрическая формула, где   — давление газа в слое, расположенном на высоте  ,   — давление на нулевом уровне ( ),   — молярная масса газа,   — газовая постоянная,   — абсолютная температура. Из барометрической формулы следует, что концентрация молекул   (или плотность газа) убывает с высотой по тому же закону: