20) Векторная диаграмма колебательного движения и ее применение при сложении одинаково направленных колебаний.( навряд ли правильно)

Часто при рассмотрении колебательных процессов оказывается удобным геометрический способ их представления с помощью векторной диаграммы. Этот способ заключается в следующем:

Возьмем некоторую горизонтальную ось X и выберем на ней произвольную точку O. Из этой точки под углом α₀, равным начальной фазе, построим в определенном масштабе вектор A, длина которого равна амплитуде колебаний. Проекция этого вектора на ось X, как видно из рису нка, дает в том же масштабе начальное смещение точки x = A cosα. Будем вращать вектор амплитуды с угловой скоростью ω₀ против часовой стрелки.В произвольный момент времени t вектор A образует с осью X угол, равный фазе (ω₀t + α₀ ), а его проекция на ось X будет x=Acos(ω₀t+α₀), т.е. равна смещению колеблющейся точки в момент времени t .

В то время как конец вектора совершит один полный оборот по окружности с угловой скоростью ω₀, его проекция осуществит полное колебание вдоль диаметра.Таким образом, гармоническое колебательное движение представляется движением проекции на некоторую ось вектора A, который отложен из произвольной точки оси под углом, равным начальной фазе, и вращается с угловой скоростью ω₀ вокруг этой точки. Поскольку угловая скорость вращения измеряется в радианах в секунду

(ω₀=2π/T), то количество колебаний в секунду проекции вектора (частота его колебаний) ν =1/T=ω₀/(2π ).

Таким образом, угловая скорость характеризует количество колебаний за время 2π с, которые совершает проекция вектора A, поворачивающегося по окружности, на диаметр. Отсюда понятно, почему величину ω₀ называют круговой или циклической частотой.

21) Динамика колебательного движения: физический маятник, пружинный маятник, энергия колебания(её сами ищите, я не умею интернетом пользоваться)

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

22) Затухающие колебания. Уравнение, коэффициент затухания, логарифмический декремент затухания.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида   в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний   или её квадрата.

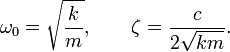
, β— коэффициент затухания.

Логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.