Бесконечная равномерно заряженная нить

Пусть τ — линейная плотность заряда нити. Выделим участок нити длиной Δl и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 5).

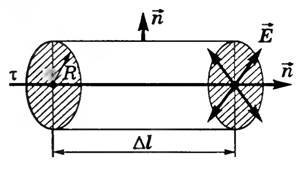
Рис. 5

Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность  , где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный поток напряженности через выделенный цилиндр

Заряд, находящийся внутри этого цилиндра, q = τ · Δl.

Согласно теореме Остроградского—Гаусса, можно записать   . Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее,

Для сферической поверхности.

Пусть поле создается точечным электрическим зарядом q. Проведем замкнутую сферическую поверхность площадью S (рис. 2), окружающую этот заряд, центр которой совпадает с точкой нахождения заряда. Вычислим поток вектора напряженности через эту поверхность. За положительное направление нормали выберем направление внешней нормали  . В этом случае во всех точках сферической поверхности E = const и cos α = 1.

Модуль напряженности поля на расстоянии R от заряда  . Площадь поверхности сферы  .

Следовательно, поток вектора напряженности через сферическую поверхность

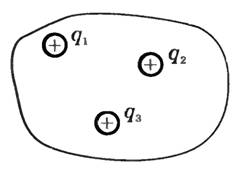
Полученный результат будет справедлив и для поверхности произвольной формы, а также при любом расположении заряда внутри этой поверхности. Действительно, если окружить сферу произвольной замкнутой поверхностью (рис. 2, а — поверхность изображена штрихами), то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Для точечного заряда.

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 2, б), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в поверхность, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линии, входящей в поверхность. Если же внутри поверхности площадью S₁ (см. рис. 2) заряды отсутствуют, то поток напряженности через эту поверхность равен нулю (N_S = 0).

42**Циркуляция вектора напряженности электростатического поля.

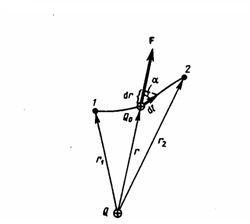
Заряд q₀ перемещается из т.1 в т.2 в поле, созданном неподвижным зарядом q.

dl – элементарное перемещение

Элементарная работа силы на элементарном перемещении равна:

Опустим перпендикуляр из конца вектора dl на продолжение r, тогда

Работа по перемещению q₀ из 1 в 2:

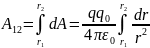
Следствие: работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому контуру равна нулю.

43.Потенциал электростатического поля. Принцип суперпозиции потенциала.

Потенциал – есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещённого в эту точку.

Принцип суперпозиции потенциалов.

Потенциал поля, созданного множеством заряов, находящихся как алгебраическая сумма потенциалов созданного каждым зарядом в отдельности в этой точке.