38.Электрический заряд. Дискретность заряда. Закон сохранения электрического заряда. Закон Кулона.

Электрический заряд – физическая величина, характеризующая взаимодействие между частицами, создающими электронное поле.

Барионный заряд – характеризует возможность барионов участвовать в сильном взаимодействии.

Закон сохранения заряда: Алгебраическая сумма электрических зарядов любой замкнутой системы остаётся неизменной, какие бы процесс ни происходили внутри.

Закон Кулона:

39.Электростатическое поле. Напряженность электростатического поля. Принцип суперпозиции электростатических полей. Поле диполя.

Электрическое поле — особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела.

Напряжённость электростатического поля – есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещённый в точку поля.

Принцип суперпозиции электростатических полей:

Напряжённость результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряжённостей полей, создаваемых в данной точке каждым из зарядов в отдельности:

Поле диполя:

Электрический диполь – система двух равных по модулю разноимённых точечных зарядов, расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля.

Плечо диполя – вектор, направленный по оси диполя(прямой, проходящей через оба заряда), от отрицательного заряда к положительному и равный расстоянию между ними.

Дипольный момент – вектор, совпадающий по направлению с плечом диполя и равный произведению заряда на плечо.

40.Поток вектора напряженности электростатического поля.**Теорема Остроградского-Гаусса для электростатического поля в вакууме.

Теорема Остроградского – Гаусса:

Поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключённых внутри этой поверхности, делённой на

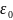
Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.

Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).

Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).

где   - угол между силовой линией и нормалью   к площадке dS;   - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

Так как   , то

где   - проекция вектора   на нормаль и к поверхности dS.

41.***Применение теоремы о-г к расчету некоторых электростатических полей в вакууме (точечного заряда, бесконечных плоскости и нити, сферы). Равномерно заряженная бесконечная плоскость

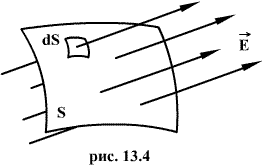
Пусть σ — поверхностная плотность заряда на плоскости (рис. 4).

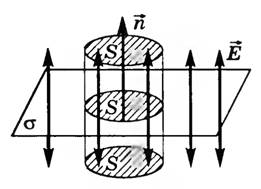
Рис. 4

В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса,  , где ε = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости