29.Халықаралық,мемлекетаралық,ұлттық эталондар.

Эталондар жалпылама 3-ке бөлінеді:халықаралық,ұлттық(мемлекеттік),мемлекетаралық.

Мемлекеттік эталондарды халықаралық эталондармен түйістіріп салыстырады.Сол кезде мемлекеттік эталондарда ұлттық деп атайды.

Мемлекеттік эталондар:1) Бірінші реттік. 2) Арнайы.

Бірінші реттік эталондар бірліктің размерін мемлекет деңгейінде ең үлкен дәлдікпен беруге арналған, арнайы орындарда сақталады, саны жалқы.

Екінші реттік эталондардың қолданылуының себептері:

1)Бірінші реттік эталондардың мезгілінен тозып кетпеуін қамтамасыз етеді.

2) Сенімдеу жұмыстарын рационалды жүргізу.

3) Эталондарды түйістіріп салыстыруды қамтамасыз ету .

4) Эталондарды сақтайтын және жаңғыртатын бірліктің размерлерінің өзгермеуін қамтамасыз етеді.

Екінші реттік эталондар :

1)Эталон көшірмелер

2) салыстыру эталондары

Эталон көшірмелерден бірліктің размері жұмысшы эталондарға беріледі. Салыстыру эталондары эталондарды өзара салыстырып түйістіруге керек.

30. Өлшеудің негізгі теңдеуін қорыту.

Өлшемдері бір -біріне тәуелсіз, ерікті түрде тағайындалатын шаманы негізгі физикалық шама,ал олардың өлшем бірліктері негізгі бірліктер деп аталады.

Өлшемдері физика заңдарымен немесе физикалық шамалардың анықтамаларымен сипатталатын және негізгі өлшемдермен өрнектелетін бірліктерді туынды бірліктер деп атайды.

1метр

1,25метр

-өлшеудің негізгі теңдеуі.

-белгілі деп есептейіk

2-мысал:

10см

31. Метрологияның аксиомалары (постулаттары).

Метрологияның негізгі постулаты: , Q-белгісіз шама, [Q]-белгілі шама.

Метрологияның аксиомалары:

1. аксиомасы: апреорлы информациясыз өлшеуді жүргізу мүмкін емес.

2. аксиомасы: өлшеу процесі- бұл салыстыру.

3. аксиомасы: өлшеу нәтижелері кездейсоқ сан болып табылады.

32. Гауус функциясының қасиеттері.

х₁, х₂, х₃, х₄, ... х₁₀₀

Өлшеулер нәтижелерін интервалдарға бөліп тастаймыз және әр интервалға сәйкес келетін эксперимент санын есептейміз.

n_i жекелеген өлшеулер нәтижелерінің саны

<x> арифметикалық орта мән; байқалу ықтималдығы, өлшеу мәнінің берілген интервалдағы байқалу мәні

L – интервалдың қадамы

К – шаманың жекелеген мәндерінің берілген ықтималдықтарда байқалу ықтималдықтарының таралуы.

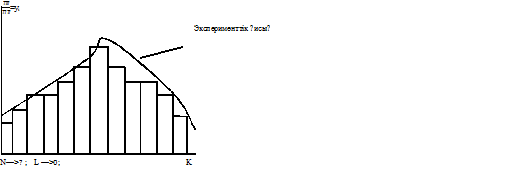
Олай болса дискретті сызықтар үздіксіз қисықөа ұмтылады.

f(x) =y

f(x) = Гаусс таралуы

<x>=

²=D(x) = =

орташа квадраттық қателік

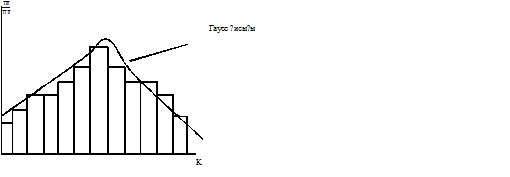
Гаусс функцияларының қасиеттері:

3. Арифметикалық орта мәні – ең ықтималды мән.

4. Арифметикалық орта мәнге салыстырғанда симметриялы.

5. Х- шаманың арифметикалық орташа мәннен ауытқуы өте үлкен болған жағдайда f(x)-ң 0-ге ұмтылуы

f(x)

Аз ауытқуының байқалу ықтималдығы жлғары, ал көп ауытқуда керісінше.

_{1 2 3}

₁- 1-ші сериялы стандарттан шыққан

₂- 2-ші ....

₁ – бүйірі шығыңқы , биіктігі үлкен

Стандартты қателіктер үлкен болған сайын Гаусс қисығының бүйірі шығыңқы, биіктігі кішкене болады.