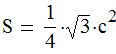7.Билет.

1.Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.

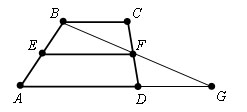
Пусть ABCD – данная трапеция.EF – средняя линия трапеции.

Проведем через вершину B и точку F прямую. Пусть эта прямая пересекает прямую AD в некоторой точке G.

Д CFB = Д FDG по второму признаку равенства треугольников (CF = FD, по построению, ∠ BCF = ∠ ПВА, как внутренние накрест лежащие при параллельных прямых ВС и DG и секущей CD, ∠ CFB = ∠ DFG, как вертикальные). Значит BC = DG и BF = FG.

Поэтому, средняя линия трапеции EF является средней линией треугольника ABG. По свойству средней линии треугольника EF || AD, а

Теорема доказана.

Свойства :средняя линия параллельна основаниям и равна их полусумме.

2.Площадь прямоугольного треугольника. Формула:

Простейшим случаем для вычисления площади, является прямоугольный треугольник. Но прежде чем определять его площадь, сформулируем понятие аддитивности площади.

Пусть мы имеем две геометрические фигуры, которые могут иметь и не иметь общих точек. Если данные фигуры пересекаются только лишь по своей границе и не имеют внутренних общих точек, то площадь двух данных фигур равна сумме площадей данных фигур в отдельности.

Теперь мы обладаем орудием для определения площади прямоугольного треугольника. Мы можем взять наш прямоугольный треугольник и построить еще один прямоугольный треугольник, в точности равный данному. Совместим полученные два треугольника по их гипотенузе, тогда мы получим прямоугольник, диагональ которого совпадает с гипотенузами совмещенных треугольников. Причем совмещенными будут только точки гипотенузы, но внутренние точки двух треугольников останутся по разные стороны от нее. Следовательно площадь полученного прямоугольника равна сумме площадей треугольников 1 и 2

Но поскольку площади данных треугольников равны между собой, то прямоугольник имеет вдвое большую площадь, чем данный прямоугольный треугольник. И наоборот площадь треугольника равна половине площади прямоугольника. Однако площадь прямоугольника гораздо проще найти. Мы привыкли с детства, что площадь прямоугольника равна произведению смежных его сторон:

Следовательно как мы сказали:

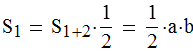
Однако учитывая теорему Пифагора, площадь прямоугольного треугольника можно рассчитать и по другой формуле:

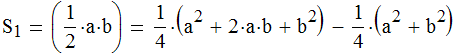
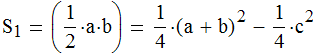
Из этого следует, что площадь прямоугольного треугольника вчетверо меньше разности площадей двух квадратов: один квадрат имеет сторону равную сумме катетов, а другой - сторону равную гипотенузе.

Из всего сказанного мы можем сделать вывод, что площадь прямоугольного треугольника вычисляется на основе понятия об аддитивности площадей фигур, не имеющих общих внутренних точек.

Площадь равнобедренного треугольника:

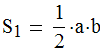
Площадь равностороннего треугольника: