Неразветвленная цепь переменного тока

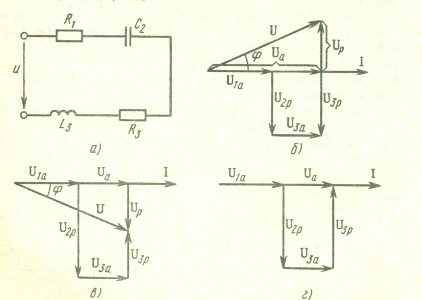
В неразветвленной цепи все элементы соединены последовательно. Особенности неразветвленных цепей и формулы для их расчета рассмотрим на примере цепи, представленной на рис. 9,а .

рис.9

Предположим, что ток в цепи выражается уравнением i=I_m sin ωt .

Мгновенное значение общего напряжения по второму закону Кирхгофа равно сумме мгновенных напряжений на элементах схемы: u=u_1a+u_2р+u_3a+u_3p (цифра индекса указывает номер элемента, буква - характер элемента: а - активный, р - реактивный).

Действующее значение общего напряжения выразим векторной суммой

U=U_1a+U_2р+U_3a+U_3p , где U_1a=IR₁; U_2р=IX₂; U_3a=IR₃; U_3p=IX₃;

X₂=1/(ωC₂); X₃=ωL

Этому уравнению соответствует векторная диаграмма на рис. 9,б. При ее построении первым нанесен вектор тока, а затем проведены векторы падения напряжения на каждом участке схемы, причем направления их относительно вектора тока определены по характеру сопротивления: активные напряжения U_1a и U_3a совпадают по фазе с током, индуктивное напряжение U_3p опережает ток на 90⁰, емкостное напряжение U_2р отстает от тока на на 90⁰ .

Векторы активного, реактивного и полного напряжений цепи на диаграмме рис.9,б образуют прямоугольный треугольник. Поэтому U=(U_а²+U_р²)^1/2, где U_а= U_1a+U_3a ;

U_р=U_3p- U_2р.

Полное сопротивление цепи Z=(R²+X²)^1/2 , где R=R₁+R₃, X=X₃-X₂ ;

Полная мощность цепи S=(P²+Q²)^1/2 =UI,

где активная мощность Р=UI cos φ = U_а I (cos φ — коэффициент мощности);

реактивная мощность Q=UI sin φ = U_рI ;

cos φ=U_a/U=R/Z=P/S ; sin φ=U_р/U=X/Z=Q/S; tg φ=U_р/U_a=X_р/R=Q/P

Эти формулы справедливы для любой неразветвленной цепи с одним источником питания. В этом случае: U_а= ∑U_R, U_р=∑U_L — ∑U_C, R=∑R_i, X=∑X_L-∑X_C, P=∑P_i , Q=∑Q_L-∑Q_C.

В зависимости от соотношения индуктивного и емкостного сопротивлений для схемы рис. 9,а возможны три случая:

3. Х>0 (Х _L > Х с) , U_L>U_C , Q>0 , угол φ>0 , напряжение цепи опережает по фазе ток (фазовые углы отсчитывают от вектора тока)— такой режим называется индуктивным (рис.9,б).

4. Х<0 (Х _L < Х с) , U_L<U_C , Q<0 , угол φ<0 , напряжение отстает по фазе от тока — такой режим называется емкостным (рис.9,в).

5. Х=0 (Х _L= Х с) , U_L=U_C , U=U_{R ,} Z=R , Q=0, угол φ=0 , напряжение и ток совпадают по фазе — такой режим называется резонансом напряжения (рис.9,г ; рис.10, а,б). Резонанс возникает при определенной частоте источника, которую называют резонансной частотой. Из условия Х _L= Х _C, или 1/(ωC)=ωL следует :

ω=1/(LC)^1/2, f= 1/(2π(LC)^1/2)

Величина реактивного сопротивления (индуктивного или емкостного) при резонансе напряжений является одной из характеристик колебательной системы. Ее называют волновым сопротивлением Zв: Zв= 1/(ω_рC)=ω_рL=(L/C)^1/2.

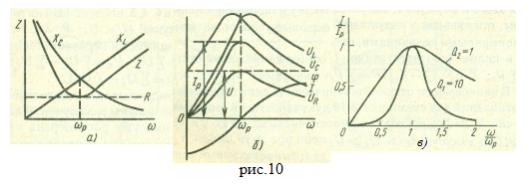
Резонансные явления широко используются в радиотехнике. Качество последовательного резонансного контура считается тем выше, чем больше отношение Q=Zв/R, которое называют добротностью контура. Чем больше мощность потерь энергии в контуре (этому соответствует меньшее значение R), тем больше добротность, тем острее резонансная кривая. На рис 10,в показаны в относительном выражении резонансные кривые при двух значениях добротности.

Пример 4: четыре последовательно соединенных участка подключены к источнику с напряжением U=217 В и частотой f=50 Гц. Сопротивления участков R₁=3 Ом, X_L1=11 Ом, R₂=4 Ом, X_C2=3 Ом, R₃= 5 Ом, X_L3=7 Ом, R₄=6 Ом, X_C4= 7 Ом. Определить : 1) ток в цепи, 2) угол сдвига фаз между напряжением и током, 3) активную, реактивную и полную мощность цепи, 5) *углы сдвига фаз между напряжениями на участках и током в цепи.

Решение:

1. Определяем активное , реактивное и полное сопротивления цепи :

R=R₁+R₂ +R₃+R₄=3+4+5+6=18 Ом ; X=(X_L1+X_L3)-(X_C2+X_C4)=11+7-3-7=8 Ом

Z=(R²+X²)^1/2=(18²+8²)^1/2=19.7 Ом

2. Определяем ток в цепи: I=U/Z=217/19.7=11 A

3. Определяем угол сдвига фаз между напряжением и током : tg φ=X/R=8/18=0.445, откуда φ=24⁰, cos φ=0.913, sin φ=0.407

4. Определяем активную, реактивную и полную мощность цепи :

Р=UI cos φ = 217·11·0.913=2179 Вт ; Q=UI sin φ = 217·11·0.407=971.5 вар

S=UI=217·11=2387 В·А

5. *Определяем сопротивление и падение напряжения на каждом участке цепи:

Z₁=(R²+X_L1²)^1/2 =(3²+11²)^1/2 =11.4 Ом ; U₁=Z₁I=11.4·11=125.4 B

Z₂=(R²+X_C2²)^1/2 =(4²+3²)^1/2 =5 Ом; U₂=Z₂I= 5·11=55 B

Z₃=(R²+X_L3²)^1/2 =(5²+7²)^1/2 =8.6 Ом; U₁=Z₁I=8.6·11=96.4 B

Z₄=(R²+X_C4²)^1/2 =(6²+7²)^1/2 =9.22 Ом; U₁=Z₁I= 9.22·11=101.4 B

6. Определяем углы сдвига фаз между напряжениями на участках и током в цепи:

tg φ₁=X₁/R₁=11/3=3.66; φ₁=74⁰40' ; tg φ₂=X₂/R₂= -3/4= -0.75; φ₂= - 36⁰50'

tg φ₃=X₃/R₃=7.5/5=1.4; φ₃=54⁰30' ; tg φ₄=X₄/R₄=-7/6=-1.166; φ₄=-49⁰30'

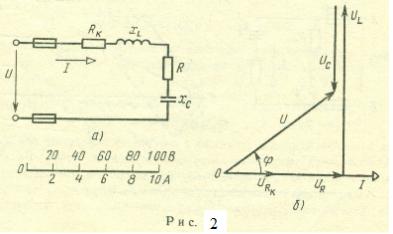
Пример 5. Неразветвленная цепь переменного тока содержит катушку с активным сопротивлением R_K = 3 Ом и индуктивным X_L = 12 Ом, активное сопротивление R = 5 Ом и конденсатор с сопротивлением Хс = 6 Ом (рис. 2, а). К цепи приложено напряжение U = 100 В (действующее значение). Определить: 1) полное сопротивление цепи; 2) ток; 3) коэффициент мощности; 4) активную, реактивную и полную мощности; 5) напряжение на каждом сопротивлении. Начертить в масштабе векторную диаграмму цепи.

Ответ: Z = 10 Ом, I = 100/10 = 10 А, sin φ = 0,6; φ = 36⁰50',cos φ = cos 36⁰50' = 0.8, Р = 800 Вт , Q = 600 вар, S = 1000 В·А , U_RK = 30 В; U_L = 120 В; U_R = 50 В; U_C = 60 В, векторная диаграмма представлена на рис. 2,б.

РАЗВЕТВЛЕННАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА

Разветвленная цепь содержит ветви, соединенные параллельно. Расчет разветвленной цепи рассмотрим на примере 6.

Пример 6. Цепь переменного тока состоит из двух ветвей, соединенных параллельно. Первая ветвь содержит катушку с активным R₁ = 12 Ом и индуктивным X_L = 16 Ом сопротивлениями; во вторую ветвь включен конденсатор с емкостным сопротивлением Хс = 8 Ом и последовательно с ним активное сопротивление R₂ = 6 Ом. Активная мощность, потребляемая первой ветвью, Р₁ = 48 Вт (рис. 3, а). Определить: 1) токи в ветвях и в неразветвленной части цепи; 2) активные и реактивные мощности цепи; 3) напряжение, приложенное к цепи; 4) угол сдвига фаз между током в неразветвленной части цепи и напряжением. Начертить в масштабе векторную диаграмму цепи.

Решение

1. Активная мощность Р₁ теряется в активном сопротивлении R₁. Поэтому Р₁= I₁²R₁. Отсюда

I₁= (P₁/R₁)^1/2=(48/12 )^1/2= 2 А.

2. Определяем напряжение, приложенное к цепи:

U_AB = I₁Z₁ = I₁(R₁²+X_L²)^1/2= 2(12² + 16² )^1/2= 40 В.

3. Определяем ток:

I₂ = U_AB/Z₂= U_AB/(R₂²+X_C²)^1/2= 40/(6² + 8² )^1/2= 4 А.

4. Находим активную и реактивную мощности, потребляемые цепью:

Р = I₁²R₁+I₂²R₂= 2²·12 + 4²·6 = 154 Вт; Q = I₁²X_L-I₂²R₂ = 2₂·16 - 4²·8 = - 64 вар .

Знак <-> показывает, что преобладает реактивная мощность емкостного характера.

Полная мощность, потребляемая цепью, S =(P²+Q²)^1/2=(154² + 64² )^1/2= 166,8 В· А.

5. Определяем ток в неразветвленной части цепи:

I = S/U_AB = 166,8/40 = 4,17 А.

6. Угол сдвига фаз во всей цепи находим через sin φ во избежание потери знака угла:

sin φ = Q/S = -64/166,8 = -0,384; φ = -22°35'.

Знак <-> подчеркивает, что ток цепи опережает напряжение U _АВ.

Для построения векторной диаграммы определяем углы сдвига фаз в ветвях:

sin φ₁ = X_L/Z₁ = 16/(12² + 16² )^1/2 = 0,8; φ₁ = 53°10';

s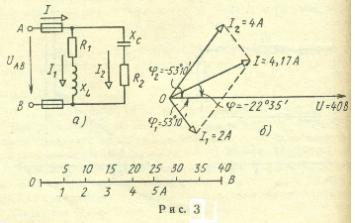 in φ₂ = X_C/Z₂ = -8/(6² + 8² )^1/2 =- 0,8; φ₂ = -53°10'.

Задаемся масштабом по току: в 1 см - 1 А и напряжению: в 1 см- 5 В. Построение начинаем с вектора напряжения (рис. 3, б). Под углом φ₁ к нему в сторону отставания откладываем в масштабе вектор тока I₁; под углом φ₂ в сторону опережения - вектор тока I₂. Геометрическая сумма этих токов равна току в неразветвленной части цепи.

** При расчете цепи с параллельным соединением ветвей можно применить метод проводимостей. По методу проводимостей ток каждой параллельной ветви рассматривают состоящим из двух составляющих: активной I_a и реактивной I_p. Вводят понятия активной G_i=R_i/ Z_i² , реактивной B_i= Х_i/Z_i² и полной Y=(G²+В²)^1/2 проводимостей, где R_i, X_i, Z_i - активное, реактивное и полное сопротивление соответствующего участка цепи.

Для примера рассмотрим цепь, представленную на рис. 11,а

Предположим, что напряжение в цепи выражается уравнением u= U_m sin ωt.

Мгновенное значение общего тока (в неразветвленной части цепи) равно сумме мгновенных значений токов в ветвях (по первому закону Кирхгофа): i=i₁+i₂+i₃=i_1а+i_2р+i_За+i_3р. Для действующих значений запишем векторную сумму I = I_1a + I_2р + I_3a + I_3p.

I_1a = I₁=U / R₁ =UG₁; I_3a =I₃ cos φ₃= UR₃/Z₃²=UG₃ ;

I_3p = I₃ sin φ₃=UX₃/ Z₃²=UB₃; I_2р = I₂ =U / Х₂= UB₂,

где G₁ = l/R₁- активная проводимость первой ветви; B₂= 1/ Х₂ - реактивная (емкостная) проводимость второй ветви; Gз=Rз/ Z₃² - активная проводимость третьей ветви; B₃=Хз/Z₃²- реактивная (индуктивная) проводимость третьей ветви.

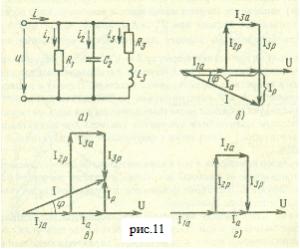
На рис.11,б представлена векторная диаграмма. При ее построении первым нанесен вектор напряжения, а затем проведены векторы активных и реактивных токов, причем учтено, что активные токи I_1a , I_3a совпадают по фазе с напряжением , индуктивный ток I_3p отстает от напряжения, а емкостной ток I_2р опережает напряжение на 90⁰.

Из векторной диаграммы получаем , что полный ток I=(I_а²+I_р²)^1/2, где

I_а= I_1a+I_3a ; I_р=I_3p - I_2р =I_3L - I_2C .

Полная проводимость цепи Y=(G²+В²)^1/2 , где G=G₁+G₃, B=B₃-B₂ ;

Полная мощность цепи S=(P²+Q²)^1/2, где активная мощность Р=UI cos φ

(cos φ — коэффициент мощности); реактивная мощность Q=UI sin φ

Полная мощность цепи S=UI.

Для любой разветвленной цепи с двумя узловыми точками, одним источником питания и произвольным количеством ветвей, содержащих резисторы, индуктивные катушки и конденсаторы получаем аналогичные расчетные формулы, с учетом того, что

I_а= ∑I_G, I_р=∑I_L — ∑I_C, G=∑G_i, B=∑B_L-∑B_C, P=∑P_i , Q=∑Q_L-∑Q_C.

В зависимости от соотношения индуктивной и емкостной проводимости для схемы рис. 11, а возможны три случая.

1. При В_L>В_С, векторная диаграмма уже рассмотрена по рис. 11, б. В данном случае

I_L > I_С, поэтому общий ток отстает по фазе от напряжения на угол φ > 0 (фазовые углы отсчитывают от вектора тока).

2. При В_L < В_С I _L< I _С , поэтому общий ток опережает напряжение на угол φ<0 (рис. 11, в).

3. При В_L=В_С I _L= I _С, но находятся в противофазе (рис. 11, г). Реактивные ток, проводимость и мощность всей цепи равны нулю; полная проводимость Y=G, а напряжение U=I/G; общее напряжение совпадает по фазе с током ( φ = О). В данном случае рассматриваемая цепь находится в режиме резонанса токов.

Явление резонанса в участке электрической цепи, содержащем индуктивный и емкостный элементы, соединенные параллельно, называется резонансом тока.

Предположим, что в схеме рис. 11, а активное сопротивление третьей ветви Rз=0, тогда реактивная проводимость этой ветви В_з=В_L= l/(ωL).

Из условия резонанса токов В_L=В_С или или 1/(ωC)=ωL получим выражение резонансной частоты, такое же, как для режима резонанса напряжений:

ω=1/(LC)^1/2, f= 1/(2π(LC)^1/2)

Величина реактивной проводимости (индуктивной или емкостной) при резонансе токов является одной из характеристик колебательной системы. Ее называют волновой проводимостью Yв:

Yв= ω_рC=1/(ω_рL)=(C/L)^1/2. На рис. 12 показаны частотные характеристики такого параллельного контура.

П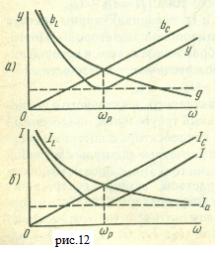 ри резонансе токов общая проводимость цепи наименьшая и равна активной проводимости цепи Y_B=G, поэтому ток в цепи наименьший.

При Y_B>G токи в реактивных ветвях схемы больше тока в неразветвленной ее части. Качество параллельного контура считают тем выше, чем больше его добротность Q, которую определяют отношением проводимостей - волновой к активной Q= Y_В/G=R/(ω_рL)=ω_рCR.

Из этой формулы также следует, что при меньших потерях энергии в цепи (этому соответствуют большие значения сопротивления R) добротность контура выше.