Цепи с активным и реактивным элементами

Индуктивная катушка и конденсатор в реальном исполнении отличаются от идеальных тем, что в них при переменном токе наряду с изменением энергии поля часть электрической энергии преобразуется в другой вид энергии. В частности, в проводе катушки электрическая энергия преобразуется в теплоту согласно закону Джоуля - Ленца . В конденсаторе кроме тока смещения есть небольшие токи проводимости (объемный и поверхностный), которые вместе с изменением поляризации вызывают потери энергии и выделение теплоты.

Поэтому схемой замещения катушки индуктивности является схема с последовательным соединением активного R и индуктивного X_L сопротивлений. А схемой замещения конденсатора является схема с последовательным (или параллельным) соединением активного R и емкостного X_С сопротивлений.

1. Цепь с сопротивлением и индуктивностью (rl цепь)

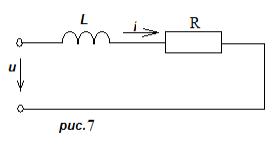
Приложенное к катушке напряжение и можно представить состоящим из двух слагаемых:

u=Ri+Ldi/dt=u_a+u_L .

Первое из них u_a= Ri называется активной составляющей напряжения, а второе

u_L = Ldi/dt=-e_L - индуктивной (реактивной)составляющей напряжения. Активная составляющая равна падению напряжения в активном элементе, а индуктивная - уравновешивает ЭДС самоиндукции. Оба напряжения изменяются синусоидально. Первое из них совпадает по фазе с током, а второе опережает его на 90⁰.

Для действующих значений выполняется векторное равенство U=U_R+U_L.

Для определения вектора U построим векторную диаграмму.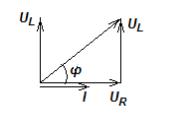

Вдоль положительного направления оси направляем вектор тока I . Вектор U_R совпадает по направлению , а вектор U_L опережает его на 90⁰.

На векторной диаграмме видно, что вектор напряжения на индуктивной катушке опережает по фазе вектор тока на угол φ. При заданном уравнении тока i=I_m sin ωt

уравнение напряжения можно записать на основе векторной диаграммы

u= U_m sin (ωt + φ).

Значение напряжения выражает гипотенуза прямоугольного треугольника, катетами которого являются векторы падения напряжения в активном и индуктивном элементах схемы

U=(U_R²+U_L²)^1/2

При последовательном соединении ток на отдельных участках цепи одинаковый I=I_R=I_L, поэтому U= I (R²+X_L²)^1/2. Так как U= IZ, где Z — полное сопротивление RL цепи, то Z=(R²+X_L²)^1/2.

Закон Ома для амплитудных и действующих значений имеет вид:

I=U/Z, I_m=U_m/Z

Графически полное сопротивление Z изображают гипотенузой прямоуголь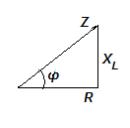 ного треугольника сопротивлений, катетами которого являются сопротивления R и X_L= Lω . Треугольник сопротивлений можно получить уменьшив в I раз треугольник напряжений.

Мгновенная мощность p= ui= U_m sin ( ωt+φ) · I_m sin ωt= UI cos φ - UI cos (2ωt + φ).

Ее можно представить в виде суммы мощностей p= p_a +p_L.

Мгновенная мощность в резистивном элементе p_a=iu_a =2U_aIsin²ωt характеризует скорость необратимого преобразования электрической энергии в какой-либо другой вид энергии, например в тепловую.

Средняя за период или активная мощность Р=UI cos φ = U_а I ,

где cos φ — коэффициент мощности.

Мгновенная мощность в индуктивном элементе p_L=iu_L = IU_Lsin 2ωt .

Реактивная индуктивная мощность цепи является мерой обменной энергии между источником питания и цепью

Q_L=UI sin φ = U_L I .

Произведение действующих значений напряжения и тока называется полной мощностью:

S=UI. Единица полной мощности называется вольт-ампер (В·А).

Активная реактивная и полная мощности графически изображаются с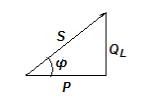 торонами прямоугольного треугольника мощностей, так как эти мощности связаны соотношением:

S²=P²+Q_L²

Угол φ (сдвиг фаз между током и напряжением ) можно определить из векторной диаграммы, треугольников сопротивлений и мощностей:

cos φ=U_a/U=R/Z=P/S

sin φ=U_L/U=X_L/Z=Q/S