2. Цепь с конденсатором

Для схемы такой цепи (рис. 5) заданы емкость С и напряжение, изменяющееся по закону u= U_m sin ωt.

Требуется определить ток в конденсаторе I, мощность цепи .

При изменении напряжения между обкладками идеального конденсатора образуется ток смещения i, который изменяется по закону i=Cdu/dt.

i=Cd(U_m sin ωt)/dt=ωС U_msin( ωt+π/2)

i=I_msin( ωt+π/2), где I_m=ωС U_m- амплитудное значение тока.

Величину 1/(Cω) – обозначают X_C и называют емкостным сопротивлением.

X_С= 1/(Сω) U_m=I_mX_С U=IX_С

Из сравнения уравнений u= U_m sinωt и i=I_m sin( ωt+π/2) видно, что между током и напряжением существует сдвиг фаз. Ток опережает напряжение на π/2 (90⁰), поэтому

векторная диаграмма будет выглядеть следующим образом: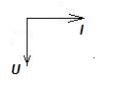

Мгновенная мощность цепи с емкостью

p= ui= U_m sin ωt · I_m sin( ωt+π/2)= (U_m I_m sin 2ωt)/2=UI sin 2ωt

Из уравнения видно, что мощность, как и в случае цепи с ин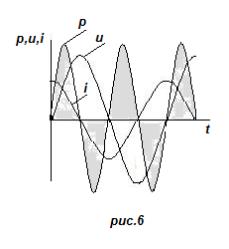 дуктивностью изменяется с двойной частотой (рис.6). Энергия, полученная цепью с конденсатором за каждый полупериод равна нулю, следовательно средняя (активная ) мощность Р=0. В рассматриваемой цепи происходит только периодический обмен энергией между источником питания и конденсатором.

Энергию, которой обмениваются источник питания и конденсатор, характеризуют максимальным значением мгновенной мощности цепи и называют ее реактивной емкостной мощностью Q_С.

Q_С=UI= U²/X_C

Пример 3 (5.80): действующее значение напряжения, приложенного к конденсатору, U=60 B, мгновенное значение тока i=3.4sin( 3140t+40⁰)А. Определить сопротивление и емкость конденсатора и записать выражение для мгновенного значения напряжения. Построить векторную диаграмму для t=0.

Решение

1. Из выражения для мгновенного значения тока имеем : I_m=3.4A, ω=3140 c^-1

2. Амплитудное значение напряжения U_m=U·2^1/2=60·1.41=84.6 B

3. С опротивление конденсатора X_С = U_m/I_m = 84.6/3.4=24.9 Ом

4. X_С= 1/(Сω) . Отсюда С= 1/( X_Сω) =1/(24.9·3140)=12.8мкФ

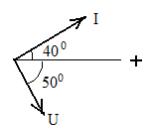
5. u= 84.6 sin(3140t +40⁰-90⁰)= 84.6 sin(3140t -50⁰)

6. для t=0 i=3.4sin(40⁰), u= - 84.6 sin(50⁰) . Векторная диаграмма представлена на рисунке.

резистор	катушка индуктивности	конденсатор
Активное сопротивление R	Реактивное сопротивление XL= Lω	Реактивное сопротивление XС= 1/(Сω)
между током и напряжением нет сдвига фаз i=Im sin ωt u= Um sin ωt	Напряжение опережает ток на π/2 (900) i=Im sin ωt u= Um sin (ωt + π/2)	Ток опережает напряжение на π/2 (900) i=Im sin ωt ; u= Um sin (ωt - π/2)
p=UI+UI sin (2ωt - л/2 ) Р=0	p= UI sin 2ωt Р=0 QL=UI= XLI2	p= UI sin 2ωt Р=0 QС=UI= U2/XC
Р — активная мощность, Вт Q- реактивная мощность, вар р — мгновенная мощность