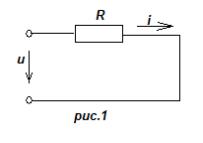
- •1. Параметры и формы представления синусоидальных тока и напряжения
- •Цепь с активным сопротивлением
- •Цепи с реактивным сопротивлением
- •2. Цепь с конденсатором
- •Цепи с активным и реактивным элементами
- •1. Цепь с сопротивлением и индуктивностью (rl цепь)
- •2 . Цепь с сопротивлением и емкостью
- •Неразветвленная цепь переменного тока
РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА
1. Параметры и формы представления синусоидальных тока и напряжения
Основная роль в развитии прикладной электротехники принадлежит переменному току. В настоящее время почти вся электрическая энергия вырабатывается в виде энергии переменного тока. Постоянный ток, необходимый в некоторых областях промышленности , транспорта, связи и т. д., получается выпрямлением переменного тока.
Основное преимущество переменного тока заключается:
в возможности просто и с малыми потерями энергии трансформировать (преобразовывать) напряжение, получая высокое напряжение для передачи электрической энергии на большие расстояния и низкое напряжение для передачи электроэнергии на близкие расстояния и для питания приемников энергии;
однофазные и трехфазные генераторы и двигатели имеют более простое устройство, надежней в работе и проще в эксплуатации по сравнению с машинами постоянного тока.
Переменным током обычно называют ток, значения которого и изменение направления повторяются в одной и той же последовательности через равные промежутки времени, называемые периодом Т . ( Период — это время одного полного колебания)
Значение переменного тока, а также напряжения, ЭДС и других изменяющихся величин в любой момент времени t называется мгновенным значением и обозначаются они строчными буквами i=i(t); и=и(t); e=e(t); q=q(t).
Колебания, совершающиеся по закону синуса (косинуса), называются гармоническими (рис.1).
Всякая величина, изменяющаяся по гармоническому закону, характеризуется :
а) амплитудой, б) частотой или периодом, в) начальной фазой.
Наибольшие из мгновенных значений периодически изменяющихся величин называются амплитудными значениями. Они обозначаются прописными буквами с индексом т, например: амплитуда тока Im, амплитуда напряжения иm; амплитуда ЭДС Em.
Число периодов в секунду, т. е. величина, обратная периоду, называется частотой переменной величины: ( частота – это число колебаний в единицу времени)
f = 1/T , герц (Гц).
Число периодов за 2π секунд, называется циклической частотой :
ω= 2πf , рад/с или с-1.
Величины, изменяющиеся по гармоническому закону, изображают синусоидами, показывающими мгновенные значения в любой момент времени, или вращающимися векторами.
С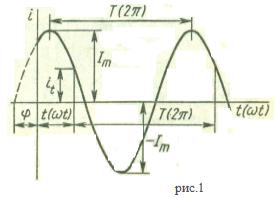 инусоиду
строят так,
чтобы
ее ординаты в выбранном масштабе
равнялись
мгновенным
значениям величины,
а
абсциссы -
времени,
отсчитанному
от некоторого момента,
выбранного
за начало отсчета (t=0).
Такое
изображение
позволяет найти амплитуду,
начальную
фазу и период .
инусоиду
строят так,
чтобы
ее ординаты в выбранном масштабе
равнялись
мгновенным
значениям величины,
а
абсциссы -
времени,
отсчитанному
от некоторого момента,
выбранного
за начало отсчета (t=0).
Такое
изображение
позволяет найти амплитуду,
начальную
фазу и период .
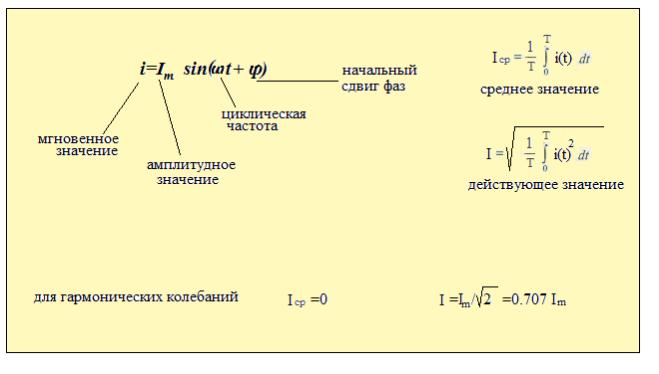
Синусоидальный ток , изображенный на рис.1 , можно представить в виде
i= Im sin( ωt +φ),
где φ- начальная фаза . Начальная фаза определяет значение тока в начальный момент времени.
(Стандартной частотой для промышленных установок в России является частота. 50 Гц. В междугородней проводной связи по воздушным линиям пользуются частотами до 150 кГц, в радиотехнике - частотами 105- 1010 Гц.)
При изображении синусоидально изменяющейся величины, например ЭДС е=е(t)=Еmsin(ωt+φ) вращающимся вектором на плоскости ху (рис. 2), длина вектора ОА в выбранном масштабе представляет амплитуду Em, угол между вектором и положительным направлением оси абсцисс х в начальный момент (t=0) равен начальной фазе φ, а угловая скорость вектора, направленная против направления движения стрелки часов, равна угловой частоте ω. Мгновенное значение е(t) определяется проекцией вектора на ось ординат у.
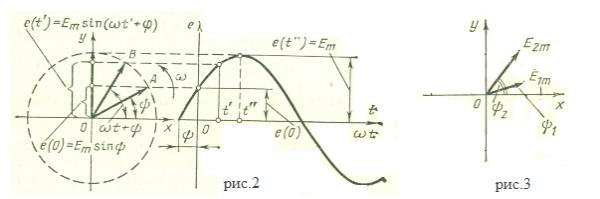
Совокупность двух или большего числа векторов, изображающих синусоидально изменяющиеся величины одной частоты в начальный момент времени (t=0), называется векторной диаграммой. На рис. 3 представлена векторная диаграмма двух ЭДС: е1=Е1msin(ωt+φ1) и е2=Е2msin(ωt+φ2).
Так как на векторных диаграммах изображают токи, ЭДС, напряжение и т. д. только одной частоты, то угловая скорость всех векторов на данной диаграмме одинакова и взаимное положение векторов в любой момент остается неизменным. При изучении гармонически изменяющихся величин, начало отсчета времени можно выбрать произвольно; поэтому на векторной диаграмме один из векторов можно направить произвольно, а остальные векторы расположить по отношению к первому под углами, равными соответствующим углам сдвига фаз, и оси координат опустить.
Изображение синусоидальных величин векторами позволяет значительно упростить графическое определение суммы или разности нескольких синусоидальных величин. Сложение векторов производят по правилу параллелограмма. Вычитание их – сложение с обратной по знаку вычитаемой величиной .
В электротехнике помимо мгновенного и амплитудного значений применяются еще понятия действующего и среднего значений.
Среднее
значение любой переменной функции f(t)
определяется п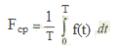 о
формуле:
о
формуле:
Для синусоидальной функции среднее значение за период равно нулю.
С![]() реднее
значение синусоидального тока Iср
вычисляют за полупериод,
в
течение которого ток остается
положительным,
т.
е.
направление
тока не изменяется.
Оно
равно такому постоянному току,
при
котором в течение полупериода проходит
тот же заряд Q,
что
и при переменном токе.
реднее
значение синусоидального тока Iср
вычисляют за полупериод,
в
течение которого ток остается
положительным,
т.
е.
направление
тока не изменяется.
Оно
равно такому постоянному току,
при
котором в течение полупериода проходит
тот же заряд Q,
что
и при переменном токе.
А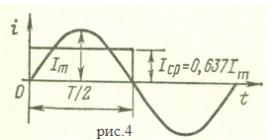 налогично
для синусоидальных напряжений и ЭДС:
налогично
для синусоидальных напряжений и ЭДС:
Uср=2Um/π ≈ 0.637Um ; Еср=2Еm/π≈ 0.637Еm; Iср=2Im/π≈ 0.637Im
Среднее за полупериод значение тока (аналогично напряжения, ЭДС) можно представить графически высотой прямоугольника с основанием, равным Т/2, и площадью, равной площади, которая ограничена осью абсцисс и кривой тока от начала до половины периода (рис. 4).
Действующие (среднеквадратичные) значения переменных величин обозначаются прописными буквами без индексов, т. е. I- ток; U - напряжение; Е - ЭДС. Действующие значения переменного тока, напряжения и ЭДС определяются по формулам:
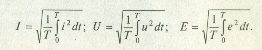
При синусоидальном токе действующие значения составляют 0.707 амплитудного значения: I= Im/21/2≈ 0.707 Im; U= Um/21/2≈ 0.707 Um ; E= Em/21/2≈ 0.707 Em
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя по цепи с тем же сопротивлением, что и переменный ток, выделяет за период то же количество тепла.
Параметрами электрических цепей переменного тока являются активное сопротивление R, индуктивность L и емкость C. Реальные элементы электрических цепей обладают всеми перечисленными параметрами, но иногда из расчетной схемы исключают те из них, влияние которых незначительно.
Рассмотрим сначала идеализированные цепи, параметрами которых являются отдельно активное сопротивление R, индуктивность L или емкость C.