Контрольные вопросы.

1. Что такое линейная цепь?

2. Как определить режим работы источника (генератор или потребитель)?

3. Что такое входное сопротивление пассивного или активного двухполюсников?

4. В чем состоит принцип суперпозиции?

5. Каков алгоритм расчета цепи методом эквивалентного генератора?

6. Что такое чувствительность?

7. Как можно использовать принцип взаимности для упрощения расчетов цепей с несколькими однотипными источниками?

8. Что такое «ветвь», «неустранимый узел», «контур»?

9. Какой принцип используют при составлении уравнений методом контурных токов и узловых потенциалов?

10. Что такое баланс мощностей?

Модуль 2. Семинар 3. «Анализ и расчет линейных цепей переменного тока»

План занятия

1. Краткое теоретическое введение

2. Разбор типовых задач.

1	Способы представления и параметры синусоидальных величин: мгновенные, векторные. Комплексные величины. Алгебраическая и полярная формы.
2	Электрические цепи с резистивным, индуктивным и емкостным элементами. Полное сопротивление.
3	Расчет простых цепей синусоидального тока
4	Сопротивления и фазовые соотношения между токами и напряжениями.

3. Самостоятельное решение задач.

4. Обсуждение самостоятельно решенных задач, включая домашнее задание

5. Краткое обобщение рассмотренных вопросов и подведение итогов

6. Следующее домашнее задание

Теоретическая часть

Анализ и расчет линейных цепей переменного тока

Периодический переменный ток, изменяющийся по синусоидальному закону со сдвигом фазы или без сдвига (рис.2), – называется гармоническим током.

Мгновенное значение гармонического тока имеет следующий вид:

i(t) = I_m sin (t +₁) = I_m cos (t + ₁ + 90^o),

где i - мгновенное значение электрического тока, А; I_m - амплитуда электрического тока, А;  - угловая частота, с^-1 ( = 2f ); f - частота, Гц; ₁ - начальный сдвиг фаза в момент времени t = 0, рад.

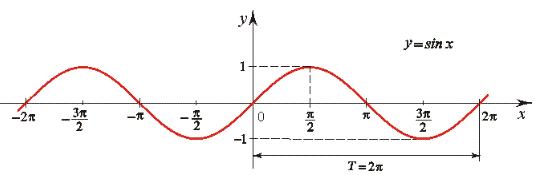
Рис. 2. График синусоидального тока

Среднее значение синусоидального тока (напряжения или ЭДС) равно:

I_ср = .

Действующее значение синусоидального тока (напряжения или ЭДС) за период T рассчитывается по формуле:

I = .

Приборами измеряются действующие значения синусоидального тока.

Рассмотрим понятия о коэффициентах амплитуды и формы.

Коэффициент амплитуды - это отношение амплитудного (максимального) значения тока (напряжения или ЭДС) к действующему значению: .

Коэффициент формы - отношение действующего значения тока (напряжения или ЭДС) к среднему значению: .

Комплексный метод расчета электрических цепей синусоидального тока. В электрических цепях синусоидального тока применяются комплексные (символические) величины для решения системы алгебраических уравнений: , Z = R +jX_р, где X_р =X_L – X_C – реактивное сопротивление и проводимость Y = g - jb_р, гдеb_р = b_L – b_C - реактивная проводимость.

При переходе от мгновенных величин (оригиналов) к комплексным величинам (изображениям оригиналов) в дифференциальных и интегральных уравнениях используется преобразование Лапласа:

; .

Соотношения между напряжением и током на элементах имеют вид: Индуктивность и конденсатора:

; u_c =

+j +j +j

90⁰ 90⁰

Рис.3. Векторные диаграммы напряжений и токов на индуктивности, конденсаторе и резистор.

Индуктивность, конденсатор и резистор ведут себя в электрических цепях синусоидального тока по-разному (рис.3). Электрический ток, проходящий через индуктивность, отстает от напряжения на 90⁰ (рис.3,а), а электрический ток, проходящий через конденсатор, опережает напряжение на 90⁰ (рис.3,б). Электрический ток, проходящий через резистор, совпадает по фазе с напряжением (рис. 3,в).

В уравнениях используется мнимая величина j = , а j² = –1, а в полярной форме (показательной) , . Умножение на j любой величины - это означает поворот вектора этой величины на 90⁰, а умножение на j² или на (-1) - это поворот вектора этой величины на 180⁰ (рис.4).

Полярная форма записи комплексного электрического тока и напряжения имеют вид , а , которые изображены на комплексной плоскости (рис.4).

Алгебраическую форму записи 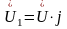комплексного числа можно получить, используя формулу Эйлера . Комплексное напряжение в алгебраической форме имеет вид:

= U cos ₂+ j Usin ₂ = Re( )+ Im( ) = a + j·b,

где a = U cos₂; b = U sin₂.

Закон Ома. Полное комплексное сопротивление можно определить, разделив комплексное напряжение на комплексный ток. Угол поворота t не влияет на расчет электрической цепи, а указывает, что эти векторы непрерывно вращаются. Поэтому величину e^jt часто не указывают при расчете схем:

,

где z - модуль полного сопротивления.

Составные элементы полного сопротивления: X_L – X_C = z sin , X_р = X_L –X_C, R = z cos .

Полное сопротивление в алгебраической форме будет Z =R + j·X_L, если электрическая цепь состоит из резистора и индуктивности, которые соединены последовательно. Их треугольник сопротивлений изображен на рис.5,а.

Полное сопротивление будет Z =R - j·X_C , если электрическая цепь состоит из резистора и конденсатора, которые соединены последовательно.