1.2.2. Метод контурных токов(мкт)

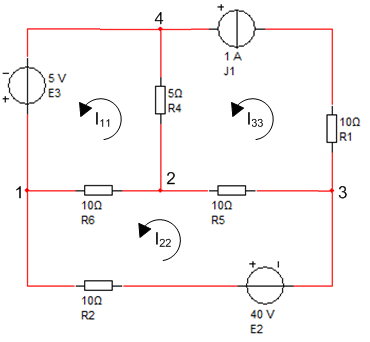
Рис. 1.2. Схема для расчета MKT

1. Задаем в каждом независимом контуре схемы свой контурный ток: I₁₁, I₂₂, I₃₃ и выбираем произвольное условно-положительное направление каждого из них (см. рис. 1.2). Выбрать направление контурных токов во всех контурах одинаковые – (по часовой стрелке или против), а направления обхода контуров - по контурным токам.

2. Составляем уравнения по второму закону Кирхгофа для каж­дого контура, которые для схемы рис. 1.2 имеют вид:

I₁₁ R₁₁ + I₂₂ R₁₂ + I₃₃ R₁₃ = Е₁₁ ,

I₁₁ R₂₁ + I₂₂ R₂₂ + I₃₃ R₂₃ = Е₂₂ , (1.3)

Здесь R₁₁иR₂₂ -собственные сопротивления первого и второго контуров, равные сумме сопротивлений соответствующих контуров.

R₁₁=R₄+ R₆= 5 Ом+10 Ом = 15 Ом; R₁₂= R₂₁= - R₆= -10 Ом;

R₂₂=R₂+R₅ + R₆= 10 Ом +10 Ом +10 Ом= 30 Ом; R₂₃= - R₅= -10 Ом;

I₃₃=J₁=1 A;R₁₃= -R₄= -5 Ом.

R₁₂, R₂₃, и R₁₃- взаимные сопротивления контуров, равные взятому со знаком минус сопротивлению ветви, смежной между контурами. Знак минус у сопротивления берется в случае несовпадения в нем направлений смежных контурных токов, знак плюс - в случае их совпадения.

Е₁₁, Е₂₂- контурные ЭДС, равные алгебраическим суммам ЭДС соответствующих контуров.

_{Е11 = Е3=5В; Е22= -Е2=-40В.}

Подставляя численные значения ЭДС, источника тока и сопротивлений, получим:

I₁₁ ·15 - I₂₂ · 10 - 5·1= 5,

-I₁₁ ·10 + I₂₂ · 30 - 10 ·1=-40.

1 5*I₁₁ -10*I₂₂= 10,

-10*I₁₁ +30*I₂₂=-30.(1.4)

Полученная система уравнений рассчитывается по методу Крамера:

I₁₁ = ∆₁₁/ ∆; I₂₂ = ∆₂₂/ ∆; I₃₃ = ∆₃₃/ ∆ ,

где ∆- определитель системы уравнений (1.4).

Соответствующие определители ∆₁₁и∆₂₂получаемые из ∆путем замены первого и второго столбцов столбцом свободных членов, равны

Найдем контурные токи:

I₁₁ = ∆₁₁/ ∆ = 0/350 = 0A;

I₂₂ = ∆₂₂/ ∆ = -350/350 = -1 A;

I₃₃=J₁=1 A.

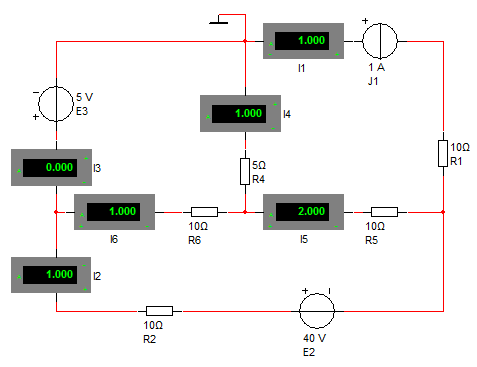
4. Значения токов в ветвях находятся как алгебраическая сумма соответствующих контурных токов. Например, ток I₆ в смежной ветви совпадает но направлению сI₁₁ и направлен навстречу I₂₂ , поэтому

I₆= I₁₁–I₂₂= 0 А + 1А = 1 А.

5. Ток I₃в несимметричной ветви (по внешней ветви) равен контурному току I₁₁.

I₃= I₁₁ = 0А;

I₁= I₃₃ = 1А;

I₂=– I₂₂ = 1А;

I₄= I₃₃– I₁₁=1А– 0А = 1А;

I₅ = I₃₃ – I₂₂=1А+1 А= 2 А.

Если бы был знак минус перед токами, то он бы показывал, что действительное их направление противоположно выбранному. MKT позволяет уменьшить число уравнений, необходимых для решения задачи до числа независимых контуров.

1.2.3. Метод узловых потенциалов (муп)

1. Полагаем потенциал одного из узлов схемы (например, узла 4) равным нулю: φ₄ = 0.Тогда потенциал φ₁ = Е₃= 5 В

2. Для остальных узлов составляем уравнения вида:

φ ₁G₂₁ +φ₂G₂₂ + φ₃G₂₃ = I₂₂ – для узла 2;

φ₁G₃₁ +φ₂G₃₂ + φ₃G₃₃ = I₃₃ – для узла 3. (1.5)

Здесь и сумма проводимостей ветвей, образующих узлы 2,3:

, , - взяты со знаком минус суммы проводимости ветвей, соединяющих соответственно узлы: 2 и 1,2 и 3,3 и 1:

, -узловые токи, равные алгебраическим суммам ЭДС ветвей, подходящих к соответствующему узлу, деленному на сопротивление этих ветвей. В эту сумму со знаком плюс входят ЭДС, направленные к узлу, и со знаком минус ЭДС,направленные от узла:

;

3. В числовых значениях система уравнений 1.5 записывается:

Решение системы уравнений дает результат:

4.Заключительным этапом является расчет токов ветвей по обобщенному закону Ома, где ЭДС и напряжение на зажимах каждой ветви берутся со знаком плюс, если они совпадают по направлению с током ветви, и со знаком минус, если они не совпадают:

_{- по первому закону Кирхгофа}

I₁=J₁=1 A