Классический метод расчета переходных процессов

1.3.1. Подключение цепи с RL-элементами к источнику постоянного напряжения

Для электрической цепи (рис.1.4) можно составить систему уравнений:

i ₁ = i₂ +i₃;

u_L +i₃·R₃ = E;

i₂ · R₂ = E.

Электрический ток второй ветви равен: i₂ =E / R₂.

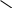
SA1 (TD) R₃

E₁ R₂ L

Рис. 1.4. Подключение RL-цепи к источнику постоянного тока.

Для вычисления тока в третьей ветви необходимо решить дифференциальное уравнение первого порядка:

.

Электрический ток определяется в виде суммы двух составляющих:

i₃ (t) =i_пр + i_св.

Здесь: i_пр - принужленный ток; i_св – свободный ток; постоянная времени .

Свободный ток равен: .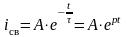

Принужденный ток равен .

Значение тока в третьей ветви получили из решения дифференциального уравнения:

.

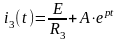Примечание. В природе свободное напряжение или свободный ток невозможно увидеть. Свободное напряжение или ток получаются при решении дифференциального уравнения справой частью равной нулю. Это только математический прием. На осциллограмме можно измерить напряжение или ток переходного процесса, а также до и после установившие значения, а свободное напряжение или свободный ток можно только вычислить.

Используя законы коммутации, найдем постоянную интегрирования:

; Тогда ;

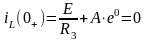Находим .

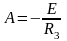Уравнение тока в третьей ветви, проходящий через индуктивность будет:

Определим напряжение на индуктивности:

.

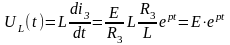Отключение цепи с rl-элементами от источника постоянного напряжения

При отключении катушки индуктивности с накопленной энергией на контактах выключателя возникнет электрическая дуга, что приведет к повреждению контактов. Переходный процесс пройдет очень быстро и окажется сложным из-за нелинейного сопротивления дуги. Другая неприятность – это ЭДС и напряжение на катушке импульсно возрастут в несколько раз больше источника постоянного напряжения, что может привести к пробою изоляции на катушке.

Для предотвращения этих неприятностей индуктивность отключается на разрядное сопротивление R_р (рис.1.5), которое включается параллельно индуктивности.

SA1 (TD) R₃

E₁ R₂ L

Рис. 1.5. Отключение RL-цепи от источника постоянного тока

Запишем дифференциальное уравнение при отключении индуктивности на разрядное сопротивление R₂ = R_р:

.

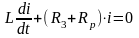Решение этого дифференциального уравнения будет состоять только из свободного затухающего тока:

.

Постоянную интегрирования можно определить:

.

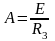Уравнение переходного процесса электрического тока определяется по формуле

.

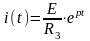Постоянная времени равна .

Напряжение на индуктивности можно определить по формуле

.

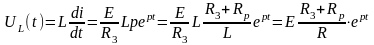Осциллограмма переходного процесса представлена на рис.1.6.

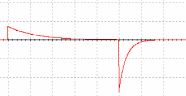
Рис. 1.6. Осциллограмма переходного процесса напряжения на индуктивности при подключении и отключении источника на разрядное сопротивление цепи с RL-элементами

1.3.3. Переходные процессы в цепях с rc-элементами

Решение задачи (рис.1.7) сводится к следующему:

• систему уравнения в интегральной или дифференциальной форме можно составить по законам Кирхгофа;

• методом замены переменных можно получить одно дифференциальное уравнение первого порядка и решить его.

R ₁ R₃

E ₁ R₂ C

Р ис. 1.7. Исследование переходных процессов электрической схемы с RС-элементами

Система уравнений для электрической цепи составляется по уравнениям Кихгофа (см. рис.1.7):

Заменяя переменные, получим следующие уравнения:

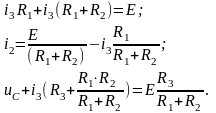
Во второй ветви ток проходит через конденсатор, значит зависимость между током и напряжением дифференциальная:

.

Получили дифференциальное уравнение первого порядка с разделяющимися переменными:

.

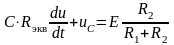Здесь: 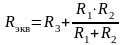; τ = СּR_экв .

Решение дифференциального уравнения найдем, как общее (правая часть равняется нулю), так и частное, зная функцию правой чести. Разделение на две составляющие напряжения на конденсаторе – это исходит только из математического решения дифференциального уравнения:

.

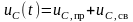Здесь u_C,пр - принужденное напряжение на конденсаторе; u_C,св - свободное напряжение на конденсаторе.

Пример. Найти численное решение электрической схемы (см. рис.1.7)

Дано: E = 60 B; R = 10 Ом (все); С = 20 мкФ.

Определить: i =? u =? τ =?

Численное значение переходного процесса напряжения на конденсаторе будет:

,

где 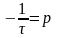или .

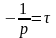Графики переходных процессов i₁(t), i₂(t), i₃(t), u_С(t), изображены на осциллограмме (рис.1.8).

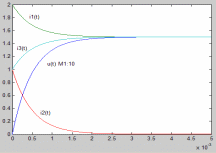
Рис. 1.8. Графики переходного процесса напряжения на конденсаторе и токов в ветвях электрической цепи (см. рис.1.7)

Уравнения переходных процессов токов в ветвях будут:

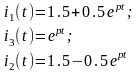
Расчет постоянной времени. Постоянную времени можно определять, используя новую переменную (jω = p) которая такая же, как сопротивления в цепи синусоидального тока:

Z_L = jωL = pL; Z_R = R.

При определении постоянной времени источники в электрической цепи должны быть равны нулю, при этом сохраняется их внутренние сопротивления и конфигурацию цепи. Эта схема эквивалентна той, что из электрической цепи удалены источники напряжения и тока, а цепь замыкаю в том месте, где удалили источник напряжения, так как внутреннее сопротивление этого источника равно нулю. Если удаляют источник тока, тогда в этом месте цепь разрывают, так как внутреннее сопротивление источника тока равно бесконечности. Ключ устанавливают в положение после коммутации. Затем определяют переменную p, а далее постоянную времени .
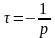