
- •1. Определение неопределенного интеграла
- •2. Определение первообразной от непрерывной функции
- •12. Определение дробно рациональной функции. Понятие правильной и неправильной рациональной функции. Простейшие дроби вида 1-4.
- •17. Вычисление интегралов от тригонометрических функций.
- •1 Двойной интеграл
- •2 Условие существования
- •3 Основные св-ва 2ного интеграла
- •4 Сведение
- •2Ного интеграла к повторному
- •5 Замена переменных в двойном интеграле. Общий случай криволинейных координат
- •6 Двойной интеграл
- •9 Вычисление
- •10 Вычисление массы,
- •11 Тройные интегралы
- •12 Замена переменных
- •13 Приложения
- •14 Определение криволинейных
- •15 Условия
- •16 Свойства криволинейных интегралов
- •17 Формула Грина
- •19 Некоторые приложения криволинейных интегралов 2 рода.
- •1 Условия независимости криволинейного интеграла 2 рода от пути интегрирования.
- •1 Интегрирование в полных дифференциалах
- •1 Сведение 2-ного интеграла к повторному
- •1 2 Ной интеграл
- •1 Замена переменных
1. ПОНЯТИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Пусть задано множество D упорядоченных пар чисел (x;y). Соответствие f, которое каждой паре чисел (x;y)€ D сопоставляет одно и только одно число z€ R, называется функцией двух переменных, определенной на множестве D со значениями в R, записывается в виде z=f(x,y) или f:D→R. При этом x и y называются независимыми переменными (аргументами), а z – зависимой переменной (функцией). Понятия функций трех и более аргументов вводятся также, как в случае двух переменных.
3. СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. 1) Функцию нескольких переменных можно задать формулой (или несколькими формулами). Функция, заданная формулой, может быть явной или неявной 2) Функцию двух или большего числа аргументов удобно задать таблицей. Для двух переменных: верхняя строка - значения одного аргумента, в первом столбце – значения другого. В пересечении – значение функции. 3) Функцию двух аргументов можно представить пространственным графиком. (см. №5)
4. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Пары тех чисел, которые (по условию вопроса) могут быть значениями аргументов х,у функции f(x,y), в совокупности составляют множество D=D(f) – область определения этой функции. Геометрически область определения изображается совокупностью точек плоскости ХОУ. Область определения трех и более числа пер-х изображается совокупностью точек в пространстве.
5. ЛИНИИ И ПОВЕРХНОСТИ УРОВНЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Поверхность. Каждой точке M0(x0,y0) области D в системе координат Oxyz соответствует точка M0(x0,y0,z0), где z0 – аппликата точки M. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию. Линия. Функцию двух переменных можно представить на плоскости по способу пометок. Пара значений х,у изображается точкой М(х,у), а значение z-числовой пометкой. Точки, для которых z имеет одно и то же значение, соединяют линией (линия уровня), при ней ставится соответствующая числовая пометка. 6.
ПРЕДЕЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Δ-Окрестность
точки точки
M0
– это все, внутренние точки круга с
центром M0
и радиусом δ. Определение.
Пусть функция z
= f(x,y)
определена в некоторой окрестности
точки M0(x0,y0),
кроме может быть, самой этой точки.
Число А называется пределом
функции z=f(x,y)
при х→х0 и у→0(или, что то же самое при
M(x:y)
→M0(х0;у0)),
если для любого ε>0 существует δ,
такое, что для всех х≠х0 и у≠у0 и
удовлетворяющих нер-ву
7. НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Функция
z=f(x,y)
или f(М))
называется непрерывной
в точке
M0(x0,y0),
если она: а)
определена в этой точке и некоторой
её окрестности б)
имеет предел
8. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 1-ГО ПОРЯДКА ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Если
сущ-ет предел
|
9. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ЧАСТНЫХ ПРОИЗВОДНЫХ 1-ГО ПОРЯДКА ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Графиком функции z=f(x,y) является некоторая поверхность. График ф-ции z=f(x;y0) есть линия пересечения этой поверх-ти с плоскостью y=y0. Исходя из геометрического смысла ф-ции одной пер-й (y= f0+f’(x0)(x-x0); f’(x0)=tg αкас=kкас), заключаем, что f’x(x0;y0) = tg αкас, где αкас – угол м/у Ox и касательной, проведенной к кривой z=f(x;y0) в т. M0[x0;y0;f(x0,y0)]. Аналогично, f’y(x0;y0)=tg β.
10. ЧАСТНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Если полное приращение ф-ции z=f(x,y) Δz=f(x,y)=f(x+Δх;y+Δy)-f(x,y) можно представить в виде Δz =АΔх+ВΔy+αΔx+βΔy, то выражения АΔх и ВΔy называют частными дифференциалами этой функции. Для независимых пер-х х и у полагают Δх=dx и Δу=dy. Поэтому рав-во полного дифференциала можно переписать в виде: dz=A∙dx+B∙dy. [Если частное приращение ф-ции z=f(x,y) Δxz=f(x,y)=f(x0+Δх,у0)-f(x0,y0) можно разбить на сумму двух членов: Δxz = AΔx + α, где А не зависит от Δx, а α имеет высший порядок относительно Δx, то первый член АΔx наз-ся частным дифференциалом функции по аргументу х и обозначается dxz.]
11. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Если полное приращение ф-ции z=f(x,y) Δz=f(x,y)=f(x+Δх;y+Δy)-f(x,y) можно представить в виде Δz =АΔх+ВΔy+αΔx+βΔy, где α=α(Δх,Δу)→0 и β=β(Δх,Δу)→0 при Δх→0, Δу→0, то сумма двух первых слагаемых в рав-ве представляет собой главную часть приращения ф-ции, которая, линейная относительно Δх и Δу, называется полным дифферециалом этой ф-ции и обозначается символом dz: dz = АΔх+ВΔy.
12.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ. Пусть z=f(x,y)
– функция двух переменных х и у, каждая
из которых является функцией независимой
переменной t:
x=x(t),
y=y(t).В
этом случае функция z=f[x(t);y(t)]
является сложной
функцией одной независимой переменной
t;
переменные х и у – промежуточные
переменные.
Теорема.
Если z=f(x,y)
– дифференцируемая в т.М(х;у)€D
функция и х=х(t)
и y=y(t)
– дифферециируемые функции независимой
переменной t,
то производная сложной функции z(t)=
f[x(t);y(t)]
вычисляется по формуле
13. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2-ГО ПОРЯДКА ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Частные
производные
14. ДИФФЕРЕНЦИАЛ 2-ГО И 3-ГО ПОРЯДКОВ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Полный
дифференциал dz
= АΔх+ВΔy
называют также дифференциалом 1-го
пор-ка. Пусть ф-ция z=f(x;y)
имеет непрерывные частные производные
2-го пор-ка. Дифференциал
2-го пор-ка
определяется по формуле
Необходимо отметить, что данные формулы справедливы лишь в случае, когда пер-е х и у ф-ции z=f(x;y) являются независимыми.
|
15.
ПОНЯТИЕ ПРОИЗВОДНОЙ ПО НАПРАВЛЕНИЮ.
Каждая из частных производных
представляет собой приращение ф-ции
вдоль соответствующей оси при неизменной
2-ой пер-й. во многих прикладных задачах
требуется определить изменение ф-ции
не только вдоль Ох или Оу, но и вдоль
любого направления на плоскости ХОУ.
Пусть ф-ция z=f(x,y)
задана в некоторой окрестности т.
М0(х0,у0) и описывает поверхность S.
Пусть l
– ось, направление которой найти. При
перемещении т. М0(х0,у0) ф-ция f(x,y)
получает приращение Δl
f=f(x,y)-f(x0,y0),
которое соотв-ет приращению Δl.
Поскольку х=х0+Δх, у=у0+Δу, то
гдеα1
и β1
– б.м. ф-ции при Δ l→0.Разделив
обе части нер-ва на
16.
ГРАДИЕНТ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Градиентом ф-ции z=f(x,y)
в т. М(х,у) назыв-ся вектор, координаты
которого равны соотв-щим частным
производным в этой точке:
17. СВОЙСТВА ГРАДИЕНТА ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. 1) grad ┴ линии уровня; 2) grad направлен в сторону возрастания ф-ции; 3) длина grad равна макс. Величине производной по направлению д-й точки, др.словами, производная по направлению принимает макс. Значение в том направлении, куда «смотрит» grad.
18. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Определение.Т. М0(х0,у0) наз-ся точкой максимума [минимума] ф-ции z=f(х,у), если сущ-ет окрестность т.М0, такая, что для всех точек с координатами (х,у) из этой окрестности выполняются усл-я: f(x0,y0)≥f(x,y); [f(x0,y0)≤f(x,y)]. Максимум и минимум ф-ции наз-ют её экстремумами. Отметим, что, в силу определения, точка экстремума ф-ции лежит внутри области определения ф-ции; максимум и минимум имеют локальный характер: значения ф-ции в т. (х0,у0) сравнивается с её значениями в точках, значительно близких к (х0,у0). В обл-ти D ф-ция может иметь несколько экстремумов и не иметь одного.
|
19. НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Пусть
т. М0(х0,у0) есть точка экстремума
дифференцируемой ф-ции z=f(x,y).
Тогда частные производные z’x(x0,y0)
и z’y(x0,y0)
равны 0. Точки, в кот-х вып-ся необходимые
условия экстремума, наз-ся критическими
или стационарными точками. В точке
экстремума grad=0.
Теорема.
Если в т. N(x0,y0)
дифференцируемая ф-ция z=f(x,y)
имеет экстремум, то её частные
производные в этой точке равны 0:
20.
ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА ФУНКЦИИ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Теорема.Пусть
в стационарной точке (x0;y0)
и некоторой её окрестности ф-ция f(x,y)
имеет непрерывные частные производные
до второго пор-ка включительно. Вычислим
в т. (x0;y0)
значения
21.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Пусть
ф-ция z=f(x,y)
определена и непрерывна в ограниченной
замкнутой области
22. ПОНЯТИЕ УСЛОВНОГО ЭКСТРЕМУМА ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. Рассмотрим задачу, в которой экстремум имеется не на всей области определения, а на множестве, удовлетворяющем некоторому усл-ю. Пусть рассматривается ф-ция z=f(x,y), аргументы х и у которой удовлетворяют условию g(x,y)=C, называемому ур-ем связи. Т. (х0;у0) называется точкой условного максимума [минимума], если существует такая окрестность, что д/всех точек окрестности выполняется неравенство f(x0;y0)≥f(x,y) [f(x0;y0)≤f(x;y)].
23.
МЕТОД ЛАГРАНЖА ОТЫСКАНИЯ УСЛОВНОГО
ЭКСТРЕМУМА ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ. Составляем ф-цию
L(x,y,λ)=f(x,y)+λ[g(x,y)-C].
Ф-ция L
наз-ся ф-цией Лагранжа, а λ – множителем
Лагранжа. Теорема.
Если т. (x0;y0)
является точкой экстремума ф-ции
z=f(x,y)
при условии g(x,y)=С,
то сущ-ет значение λ0, такое, что т.
(х0,у0,λ0) явл-ся точкой экстремума ф-ции
L(x,y,λ),
т.е. ф-ции Лагранжа. Т.о., для нахождения
условного экстремума ф-ции z=f(x,y)
при усл-и g(x,y)=C
требуется найти экстремум ф-ции L.
Последнее условие экстремума grad f = -λg*grad g, т.е. в точке экстремума градиенты ф-ций f и g коллинеарны. Замечание. В случае ф-ции многих пер-х рассм-ся больше ур-й связи, и, соответственно, больше множителей Лагранжа.
|
24.
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ НА НАЛИЧИЕ ЭКСТРЕМУМА.
Исследование ф-ции 2-х пер-х z=f(x,y)
на наличие экстремума проводится по
следующей схеме: 1.
находим частные производные z’x,
z’y;
2.
находим критические точки, решая
систему
25.
ПОНЯТИЕ КРАТНОГО ИНТЕГРАЛА. Пусть на
измеримом множестве Х 26.
ПОНЯТИЕ ДВОЙНОГО ИНТЕГРАЛА. Пусть D
– некоторая замкнутая ограниченная
обл-ть. Построим покрывающую эту
область решётку, заштрихуем ту часть,
которая не покрыта полными клетками.
Очевидно, что площадь этой части
уменьшается по мере того, как
увеличивается число клеток разбиения.
Пронумеруем клетки решётки индексами
i
и j:
27.
СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА. 1.
если C
– произвольное число, и ф-ция f(x,y)
интегрируема в обл-ти D,
то ф-ция Cf(x,y)
тоже интегрируема в D
и
28.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДВОЙНОГО
ИНТЕГРАЛА. Пусть ф-ция z=f(x,y)
непрерывна и неотрицательна в обл-ти
D.
Тогда двойной интеграл
|
30.
ПОНЯТИЕ ЭЛЕМЕНТАРНОГО МНОЖЕСТВА.
ПРИМЕРЫ. Множество
31.
ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ
(ПРЯМОУГОЛЬНАЯ ОБЛАСТЬ). Пусть обл-ть
D
задана неравенствами
32.
ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ. СЛУЧАЙ
ПРОИЗВОЛЬНОЙ ОБЛАСТИ. 1.
Если контур области D
встречается со всякой пересекающей
его вертикальной
прямой не более чем в двух точках
(М1,М2),
то обл-ть D
задаётся неравенствами
|
33.
ПРИЛОЖЕНИЯ ДВОЙНОГО ИНТЕГРАЛА. Объём
тела. Исходя
из геометрического смысла двойного
интеграла объём цилиндрического тела
находится по формуле
34. СМЕНА ПОРЯДКА ИНТЕГРИРОВАНИЯ В ДВОЙНОМ ИНТЕГРАЛЕ.
35.
ПОНЯТИЕ ТРОЙНОГО ИНТЕГРАЛА. Пусть
ф-ция u=f(x,y,z)
непрерывна внутри замкнутой
пространственной области V
и на её границе. Разобьём область V
сеткой поверхностей на части, которые
пронумеруем индексами i,
j,
k:
|
36.
СВОЙСТВА ТРОЙНОГО ИНТЕГРАЛА. Тройной
интеграл обладает теми же свойствами,
что и двойной интеграл: 1.
37.
ПРАВИЛА ВЫЧИСЛЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ.
Пусть областью интегрирования является
тело, ограниченное снизу поверхностью
z=z1(x,y),
сверху – поверхностью z=z2(x,y),
причем f(x,y)
и g(x,y)
– непрерывные ф-ции в замкнутой области
D,
являющейся проекцией тела на плоскость
Oxy.
Будем считать область V
– правильной в направлении оси Oz:
любая прямая параллельная оси Oz,
пересекает границу области не более
чем в двух точках. Тогда для любой
непрерывной в области V
ф-ции f(x,y,z)
имеет место формула
38.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ТРОЙНОГО
ИНТЕГРАЛА. Пусть ф-ция z=f(x,y,z)
непрерывна и неотрицательна в
пространственной обл-ти V.
Тогда тройной интеграл
|
1. Определение неопределенного интеграла
Если функция F(x) – первообразная для ф-ии f(x) на промежутке [a,b] , то множество ф-ий F(x)+C, где С – произвольная постоянная, называется неопределенным интегралом от ф-и f(x) на этом промежутке и обозначается символом ∫f(x)dx=F(x)+C
При этом ф-я f(x) называется подынтегральной ф-ей, f(x)dx – подынтегральным выражением, а переменная х – переменной интегрирования.
2. Определение первообразной от непрерывной функции
Функция F(x) называется первообразной для ф-ии f(x) на промежутке [a,b] , если для всех значений х из этого промежутка выполняется равенство F’(x)=f(x)
Если функция f(x), хЄ[a,b] – непрерывная, то для нее существует первообразная (неопред. Интеграл)
3. Теорема: Если ф-я F(x) является первообразной ф-ии f(x) на отрезке [a,b], то множество всех первообразных ф-ии f(x) задается формулой F(x)+C, где С-константа
Док-во: F(x)+C – первообразная, тогда (F(x)+C)’= F’(x)+C’= F’(x)=f(x)
Ф(х) – тоже первообразная: Ф’(х)=f(x), xЄ[a,b]. (Ф(х)-F(x))’= Ф’(х)-F’(x)=f(x)- f(x)=0 =>
Ф(х)-F(x)=C, С-const. Таким образом Ф(х)=F(x)+С
Почему так: ф-ия, производная которой на некотором промежутке Х равна 0, постоянна на этом промежутке.φ’(x)=0 => φ(x)=C, для каждого хЄ[a,b], тогда для каждого х1,х2 Є [a,b], х1<х2. По теореме Лангранжа: φ(x2)- φ(x1)=0, φ(x)=С
4. Выражение (∫f(x)dx)’ – Производная неопределенного интеграла = подынтегральной функции. (∫f(x)dx)’=f(x). Док-во: (∫f(x)dx)’=(F(x)+C)’= F’(x)= f(x)dx
5. Выражение ∫dF(x) – Неопределенный интеграл от дифференциала некоторой ф-ии = сумме этой ф-ии и произвольной постоянной ∫dF(x)=F(x)+C.Так как ∫dF(x)= F’(x)dx, то ∫F’(x)dx=F(x)+C
6. Если k-постоянное, ненулевое число, то ∫kf(x)dx=k∫f(x)dx – Постоянный множитель можно вынести из-под знака интеграла. Пусть F(x) – первообразная для ф-ии f(x), т.е. F’(x)=f(x), тогда kF(x)-первообразная для ф-ии kf(x): (kF(x))’=kF’(x)=kf(x). Отсюда следует: k∫f(x)dx= k[C+(x)F]=kF(x)+C1=∫kf(x)dx, где С1=kC
7. Если ∫f(x)dx=F(x)+C, то и ∫f(u)du=F(u)+C, u=φ(x) – произвольная ф-ия, непрерывн, дифферен-я. f(x)-непрерыв. => ∫f(x)dx=F(x)+C, u=φ(x)-непрерыв. дифферен.ф-я. F(u)=F(φ(x)) –согласно инвариантности первого дифференциала. Инвариантность первого дифференциала: y=f(x) dy=f’(x)dx y=f(u), u=φ(x) – непрерыв,диф-я dy=f’(x)du dF(u)=F’(u)du=f(u)du ∫f(u)du=∫d(F(u))=F(u)+C
8. Выражение d(∫f(x)dx)=f(x)dx - Дифференциал от неопределенного интеграла = подынтегральному выражению. d(∫f(x)dx)=d(F(x)+C)=dF(x)+dC=F’(x)dx+0=f(x)dx
9. Интеграл ∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx –неопределенный интеграл от алгебраической суммы двух ф-ий равен алгебраической суммы интегралов от этих ф-ий в отдельности: Пусть F(x) и G(x) – первообразные для ф-ий f(x) и g(x): ∫[f(x)+g(x)]dx=∫(F’(x)+G’(x))dx=∫(F(x)+G(x))’dx=∫d(F(x)+G(x))= F(x)+G(x)+C=F(x)+G(x)+C1+C2= F(x)+C1+G(x)+C2=∫f(x)dx+∫g(x)dx
10. Вывод формулы замены переменного в неопределенном интеграле (подстановка). Пусть ф-я x=φ(t) определена и диф-ма на некотором промежутке Т и Х-множество значений этой ф-ии, на кот. определена ф-я f(x). Тогда, если на множестве Х ф-я f(x) имеет первообразную, то на множестве Т справедлива формула: ∫f(x)dx=∫f[φ(t)]φ’(t)dt
Док-во: Пусть F(x)-первообразная для f(x) на множестве Х. Рассмотрим на множестве Т сложную ф-ю F[φ(t)]: (F[φ(t)])’=Fx’[φ(t)]φ’(t)=f[φ(t)]φ’(t), т.е. ф-я f[φ(t)]φ’(t) имеет на множестве Т первообразную F[φ(t)]=> ∫f[φ(t)]φ’(t)dt=F[φ(t)]+C, Замечая что F[φ(t)]+C=F(x)+C=∫f(x)dx, Получаем: : ∫f(x)dx=∫f[φ(t)]φ’(t)dt
11. Вывод формулы интегрирования по частям. Пусть ф-ии u(x) и v(x) определены и диф-мы на некотором промежутке Х и пусть ф-я u’(x)v(x) имеет первообразную на этом промежутке. Тогда на промежутке Х ф-я u(x)v’(x) также имеет перво-ю и справедлива формула: ∫u(x)v’(x)dx=u(x)v(x)-∫v(x)u’(x)dx. Док-во: Из равенства [u(x)v(x)]’=u’(x)v(x)+u(x)v’(x) следует что u(x)v’(x)=[u(x)v(x)]’-u’(x)v(x) Первообразной ф-ии [u(x)v(x)]’ на промежутке Х является ф-я u(x)v(x). Ф-я u’(x)v(x) имеет первообразную на Х по условию теоремы. Следовательно, и ф-я u(x)v’(x) имеет пер-ю на Х. Интегрируя последнее равенство получаем: : ∫u(x)v’(x)dx=u(x)v(x)-∫v(x)u’(x)dx. Так как v’(x)dx=dv, u’(x)dx=du, то ее можно записать в виде: ∫udv=uv-∫vdu
По лекциям: d(uv)=udv+vdu Проинтегрируем последнее соотношения: ∫d(uv)=∫udv+vdu => ∫udv=∫d(uv)-∫vdu=uv-∫vdu



 В
1-й формуле сначала вычисляется
внутренний интеграл
В
1-й формуле сначала вычисляется
внутренний интеграл
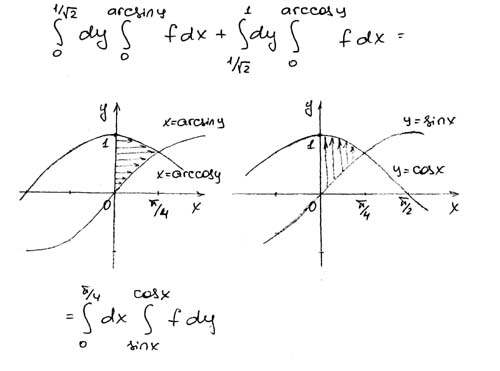

 3.
3.
 4.
Теорема (о
среднем). Если ф-ция z=f(x,y,z)
непрерывна в области V,
то в этой области найдётся такая точка
4.
Теорема (о
среднем). Если ф-ция z=f(x,y,z)
непрерывна в области V,
то в этой области найдётся такая точка
 .
В процессе вычисления интеграла
.
В процессе вычисления интеграла