3. Операторный метод расчета переходных процессов в электрических цепях.

Операторный метод основан на использовании некоторого оператора р, р является комлексным числом, p=a+jb

a-действительная часть

b-мнимая часть

f(t)-оригинал

1)

2)

3)

4)

Этапы применения метода:

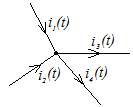
1)Обозначить положительные направления токов каждой ветви

2)Записать все оригиналы заданных величин и преобразовать их в отображение(учесть переходные процессы) прямого преобразования Лапласа или же через таблицу

3)Используя закон Ома и Кирхгофа определяют неизвестные величины (можно использовать различные методы расчетов)

4)Полученные отображения преобразуют в оригиналы путем использования обратного преобразования Лапласа или таблиц соответствия

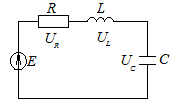
Закон Ома и Кирхгофа в операторной форме

e(t)- мгновенное значение ЭДС

В операторной форме:

4. Частотный метод расчета переходных процессов в электрических цепях.

ЧАСТОТНЫЙ (СПЕКТРАЛЬНЫЙ) МЕТОД АНАЛИЗА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

При частотном методе анализа электрическая цепь задается своими частотными ха-рактеристиками (АЧХ и ФЧХ), которые в большинстве практических случаев могут быть просто измерены или рассчитаны. При этом необходимо определить реакцию на произволь- ное (негармоническое) воздействие. Поскольку частотные характеристики являются характе- ристиками установившегося режима гармонических колебаний, то целесообразно произ- вольное воздействие представить в виде совокупности гармонических и реакцию линейной цепи искать как совокупность реакций, вызванных каждым гармоническим воздействием в отдельности. Таким образом, частотный метод анализа включает в себя задачу частотного или спектрального представления воздействия в виде суммы гармонических составляющих с определенными амплитудами, начальными фазами и частотами, а также задачу определения реакций цепи на каждую гармоническую составляющую воздействия и их суммирование.

Сформулированные задачи наиболее просто решаются для периодических негармони- ческих воздействий, которые при некоторых ограничениях могут быть представлены в виде гармонического ряда Фурье. 4.7. Спектральный метод анализа электрических

цепей

Пусть на входе некоторой линейной системы действует входной сигнал u1(t), задан- ный в виде интеграла Фурье:

(1)

Линейная система задана своими частотными характеристиками, а именно: АЧХ - |H(jω)| и ФЧХ - θ(ω). Имея в виду, что (1) является интегральной суммой гармонических составляющих, и применяя принцип суперпозиции, можно вычислить реакцию u2(t) на выходе системы с помощью частотных характеристик аналогично тому, как это было сделано для периодического воздействия. Тогда получим:

(2)

Полученное соотношение (2) является интегралом Фурье для выходного сигнала. Причем, спектральные характеристики выходного сигнала

|

Очевидно, что формулы (4.14) можно объединить в одну

где – комплексные спектральные плотности воздействия и реакции; комплексная функция передачи системы.

Таким образом, при спектральном анализе, эффект преобразования сигнала в системе отображается простой алгебраической операцией умножения. Зная АЧХ и ФЧХ цепи, можно найти спектральные характеристики и саму реакцию на любое воздействие, которое может быть представлено интегралом Фурье. Спектральный метод анализа особенно удобен, если система имеет простые (идеализированные) частотные характеристики.