СОДЕРЖАНИЕ
ВВЕДЕНИЕ.......................................................................................................................3
1 МОДЕЛЬ ХАТА-ДЕВИДСОНА ДЛЯ ПРЕДСКАЗАНИЯ УРОВНЯ
СИГНАЛА.........................................................................................................................4
1.1 Расчет модели Хата-Девидсона для предсказания уровня сигнала....................................................................................................................4
2 АЛГОРИТМ ЧАСТОТНО-ТЕРРИТОРИАЛЬНОГО ПЛАНИРОВАНИЯ СОТОВОЙ СВЯЗИ......................................................................................................................7
2.1 Расчет зоны обслуживания по формулам Эрланга.............9
3 ЗОНА ПОКРЫТИЯ НА ОСНОВЕ ДИФРАКЦИОННОЙ АНАЛИТИЧЕСКОЙ МОДЕЛИ НАПРЯЖЕННОСТИ ПОЛЯ СИГНАЛА.........................................11
3.1 Методика расчета зоны покрытия на основе дифракционной аналитической модели напряженности поля...........................12
4 МОДЕЛЬ ЛИ ДЛЯ ПРЕДСКАЗАНИЯ УРОВНЯ СИГНАЛА..................................14
4.1 Расчет модели Ли для предсказания уровня сигнала.....15
ЗАКЛЮЧЕНИЕ................................................................................................................17
БИБЛИОГРАФИЧЕСКИЙ СПИСОК......................................................18
ВВЕДЕНИЕ
Системы наземной подвижной связи – одни из наиболее быстро развивающихся в сфере телекоммуникаций. По росту числа пользователей эти системы можно сопоставить только с сетью Интернет. Подвижная связь имеет ряд принципиальных отличий от других телекоммуникационных систем, которые явились ответом на два «отягчающих» обстоятельства.
Во-первых, современные системы подвижной связи вынуждены функционировать в условиях острейшего дефицита частотного ресурса. Например, для сетей GSM-900 выделены полосы частот шириной 2х25=50 МГц. Для сравнения наземное телевидение занимает полосу более 400 МГц в близком частотном диапазоне.
Во-вторых, радиоканалы систем подвижной связи имеет, как правило, очень плохое качество. Они характеризуются глубокими замираниями сигнала, высоким уровнем помех и многолучевостью, которая в свою очередь вызывает межсимвольную интерференцию сигналов.
Современная подвижная связь стала возможной благодаря широчайшему использованию новейших научных достижений и технологий, прежде всего в области цифровой обработки сигналов, микропроцессорной техники, адаптивных систем управления.
Построение и эксплуатация различных типов систем и сетей подвижной радиосвязи требует знания принципов расчета зон покрытия и определения уровня сигнала в точке приема. Проектирование систем и сетей подвижной радиосвязи обязательно предусматривает этап размещения базовых станций и расчет зон покрытия для определения ожидаемого уровня сигнала в точке приема.
1 Модель хата-девидсона для предсказания уровня сигнала
Используя следующие уравнения можно определить потери на трассе:
при
;
(1.1)
при
;
(1.2)
при
;
(1.3)
После расчета этих коэффициентов делается перерасчет:
при
;
(1.4)
;
(1.5)
-
потери на трассе.
-
потери на трассе с расширением Девидсона.
Данная модель включает дополнительные затухания на трассе из-за дифракционных потерь.
1.1 Расчет модели Хата-Девидсона для предсказания уровня сигнала
Задание:
Рассчитать потери модели Хата-Девидсона при частоте f=1800 МГц, высота антенны hБС=50 м, hАС=7 м, расстояние – модель среднего города.
Расчет:
Используя следующее уравнение можно определить потери на трассе:
при
R>20 км,
,
где
-
для города с плотной застройкой;
коэффициенты
и
используются, чтобы учесть частотные
диапазоны:
-
для частотного диапазона
;
-
для частотного диапазона
.
При
При
При
При
При
При
По полученным данным строим график потерь на трассе в зависимости от расстояния:
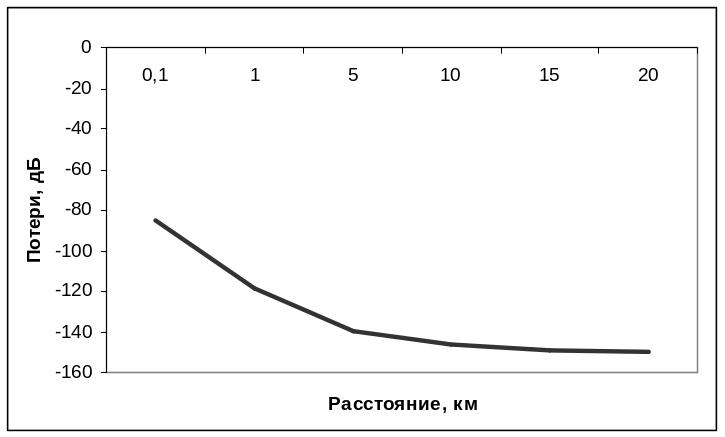
Рисунок 1 - График потерь на трассе в зависимости от расстояния
После расчета этих коэффициентов делается перерасчет по формуле:
При
При
При
При
При
При
По полученным данным строим график потерь на трассе в зависимости от расстояния:
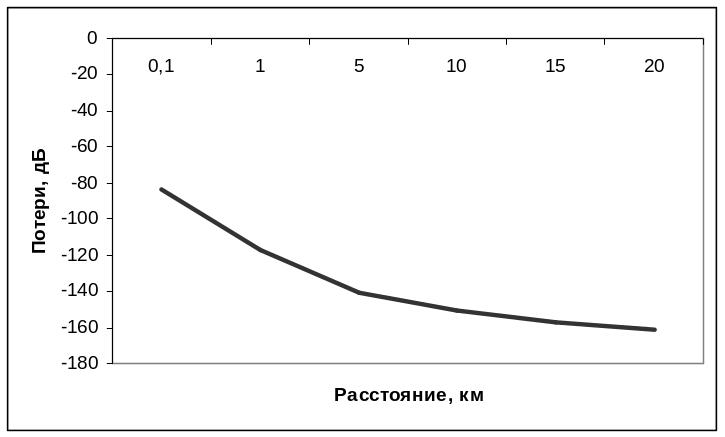
Рисунок 2 - График потерь на трассе в зависимости от расстояния
2 Алгоритм частотно-территориального планирования сотовой связи
Рассмотрим
-канальную
систему массового обслуживания с
отказами, на вход которой поступает
простейший поток заявок с плотностью
;
время обслуживания - показательное, с
параметром
.
В начале, сразу после включения системы
в работу, протекающий в ней процесс еще
не будет стационарным: в системе массового
обслуживания (как и в любой динамической
системе) возникнет так называемый
«переходный», нестационарный процесс.
Однако, спустя некоторое время, этот
переходный процесс затухнет, и система
перейдет на стационарный, так называемый
«установившийся» режим, вероятностные
характеристики которого уже не будут
зависеть от времени.
Можно
доказать, что для любой системы с отказами
такой предельный режим существует, т.
е. что при
все вероятности
стремятся к постоянным пределам
, а все их производные - к нулю.
Существует система алгебраических уравнений:
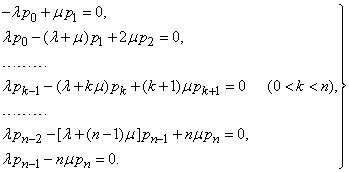(2.1)
К этим уравнениям необходимо добавить условие:
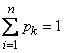(2.2)
Разрешим систему (2.1) относительно неизвестных . Из первого уравнения имеем:
(2.3)
Из второго, с учетом (2.3):
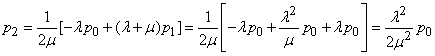(2.4)
аналогично из третьего, с учетом (2.3) и (2.4):
,
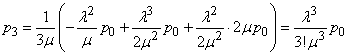и
вообще, для любого
:
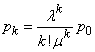(2.5)
Введем обозначение:
(2.6)
и
назовем величину
приведенной плотностью потока заявок.
Это есть не что иное, как среднее число
заявок, приходящееся на среднее время
обслуживания одной заявки. Действительно:
,
где
- среднее время обслуживания одной
заявки. В новых обозначениях формула
(2.5) примет вид:
(2.7)
Формула
(2.7) выражает все вероятности
через
.
Чтобы выразить их непосредственно через
и
,
воспользуемся условием (2.2). Подставив
в него (2.7), получим:
,
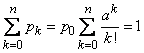откуда
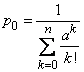(2.8)
Подставляя (2.8) в (2.7), получим окончательное выражение:
(2.9)
Формулы
(2.9) называются формулами Эрланга. Они
дают предельный закон распределения
числа занятых каналов в зависимости от
характеристик потока заявок и
производительности системы обслуживания.
Полагая в формуле (2.9)
,
получим вероятность отказа (вероятность
того, что поступившая заявка найдет все
каналы занятыми):
(2.10)
В
частности, для одноканальной системы
(
):
(2.11)
а относительная пропускная способность:
(2.12)