13. Переходная характеристика, интеграл Дюамеля
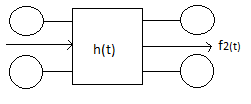
Переходной
характеристикой цепи называется
отношение реакции цепи на ступенчатые
воздействия к величине воздействия,
при нулевых начальных условиях и
обозначают
,
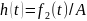где
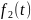- реакция цепи; А – величина ступенчатого
воздействия.
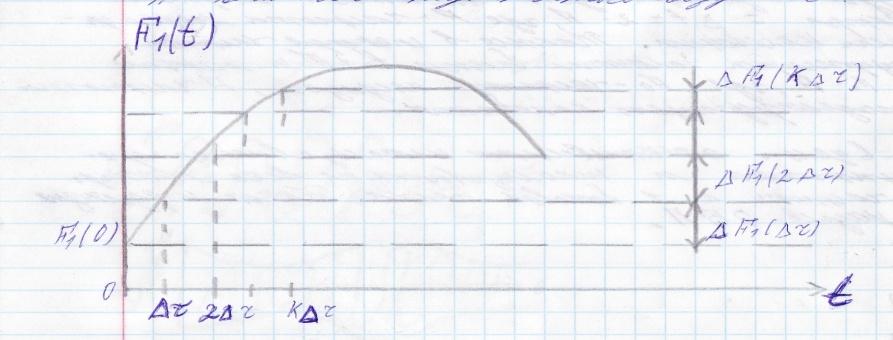
Представим f(t) в виде суммы количества ступенчатых воздействий
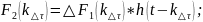
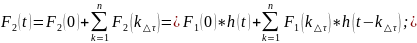
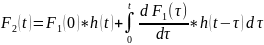
14. Алгоритм и его свойства.
Алгоритм – это точная конечная система правил, определяющая содержание и принцип действия исполнителя над некоторыми объектами. Каждое действие представления алгоритмов должно быть закончено, прежде чем он приступит к исполнению следующего действия:
Произвести каждое отдельное действие исполнителю предписывает специальное указание, называемое командой. Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было известно какую команду надо выполнить в следующем. Это свойство называется точностью.
Алгоритм может быть выполнен только исполнителем, который понимает каждую команду алгоритма и может исполнить её. Это свойство называется понятностью.
Алгоритм не должен оставлять места произвола. Это свойство называется определённостью.
Результативность; смысл этого свойства состоит в том, что при точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи.
Массовость, т.е. способность решения любой задачи из некоторого класса задач.
15. Псевдо случайные последовательности
При статическом моделировании систем идентификации одним из основных вопросов является учет стохастических возможностей воздействий. Количество случайных чисел используемых при идентификации объектов определяется процессом функционирования системы и колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик , необходимой точности и достоверности результата моделирования. Основные методы получения случайных последовательностей.
Аппаратный способ
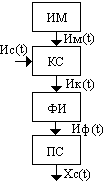
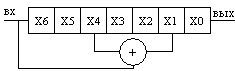
При этом способе генерации случайные числа вырабатываются датчиком случайных чисел, в качестве физического эффекта, чаще всего используются шумы в электронных лампах, полупроводниковых приборах. Рассмотрим принцип получения следующих чисел, на эффекте шумы в полупроводниковых приборах. Структурная схема аппаратного генератора случайных чисел, приведены на рисунке
ИМ – источник шума
КС – ключевая схема
ФИ – формирователь импульсов
ПС – пересчетная схема
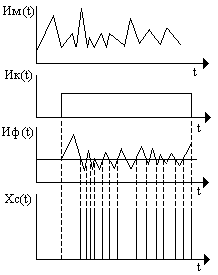
При усилении шумов на входе ИМ получается напряжение, которое является случайным процессом. Причем отрезок шумовой реализации Ик(t), сформированный интервал времени от 0 до t с помощью ключевой схемы, содержит случайное число выборов сравнения напряжения Ик(t), позволяет сформировать на выходе ФИ серию импульсов Иф(t). Тогда на выходе ПС может быть получена последовательность случайных чисел Х(t).