1. Идентификация, модели и их характеристики

Под идентификацией понимается определение структуры и параметров модели, обеспечивающих наилучшее совпадение выходных сигналов модели и объекта, при одинаковых входных воздействиях.

Модель – это представление объекта или системы в некоторой форме отличной от формы их реального существования. Модели могут принимать самую различную форму и записываться с разной степенью математической детализации. Для описания свойств некоторых объектов используют числовые таблицы или графики. Мат. модель представляет собой формализованное мат. описание, отражающее с требуемой точностью процессы, происходящие в исследуемом объекте.

Модели можно классифицировать на:

• Физические и математические

• Статические и динамические

• Детерминированные и стохастические

• Дискретные и непрерывные

• Линейные и нелинейные

• Сосредоточенные и распределенные

• Стационарные и нестационарные

2. Математические модели дискретных и непрерывных процессов

К математическим моделям относят те модели, в которых для представления процесса используется символы, а не физические устройства.

Процесс функционирования объекта во времени описывается модельным оператором F, который преобразует независимые переменные в соответствии с алгоритмом функционирования объекта.

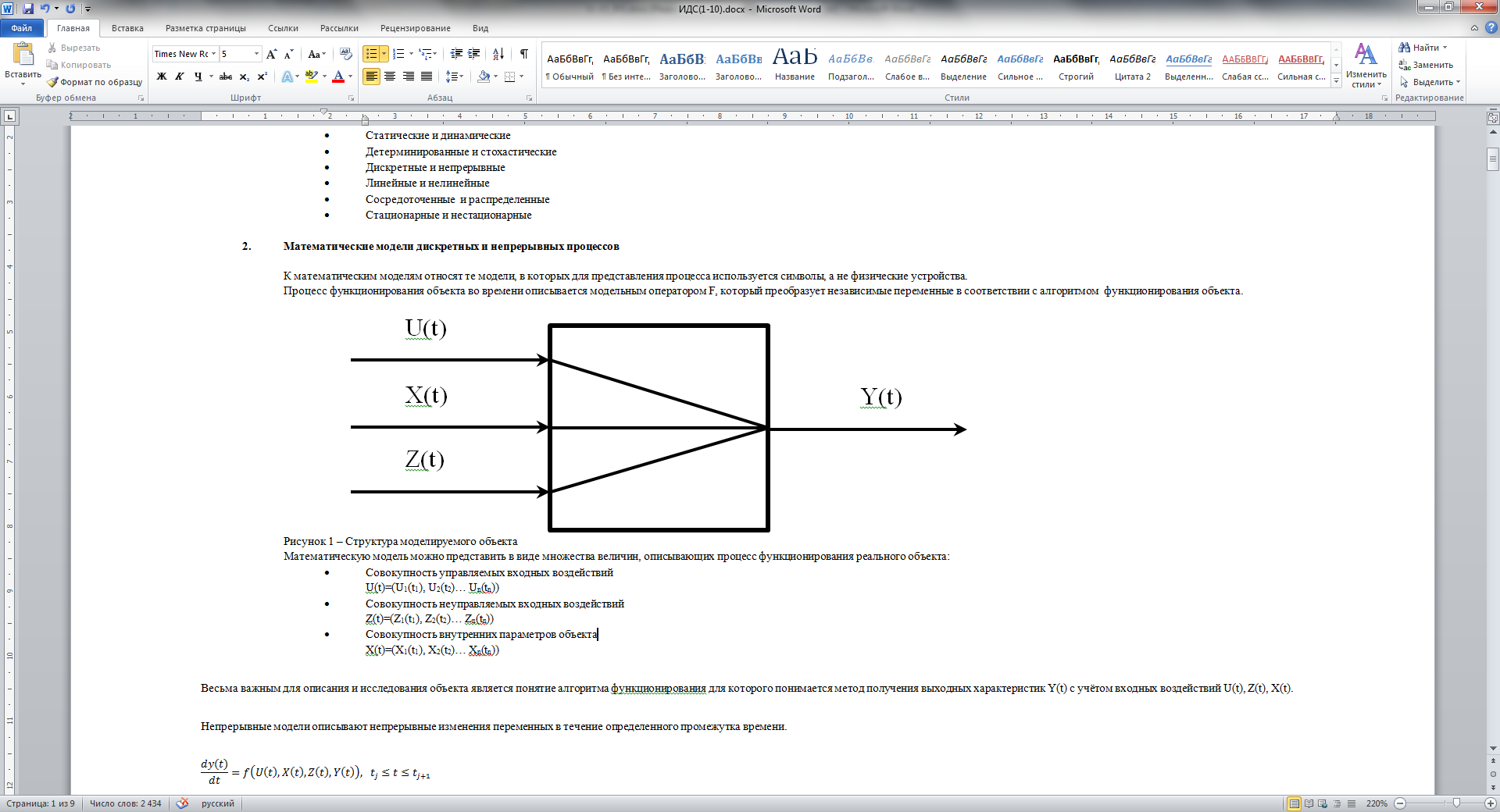
Рисунок 1 – Структура моделируемого объекта

Математическую модель можно представить в виде множества величин, описывающих процесс функционирования реального объекта:

• Совокупность управляемых входных воздействий

U(t)=(U1(t1), U2(t2)… Un(tn))

• Совокупность неуправляемых входных воздействий

Z(t)=(Z1(t1), Z2(t2)… Zn(tn))

• Совокупность внутренних параметров объекта

X(t)=(X1(t1), X2(t2)… Xn(tn))

Весьма важным для описания и исследования объекта является понятие алгоритма функционирования для которого понимается метод получения выходных характеристик Y(t) с учётом входных воздействий U(t), Z(t), X(t).

Непрерывные модели описывают непрерывные изменения переменных в течение определенного промежутка времени.

Дискретная модель описывает зависимость между переменными объекта в дискретные моменты времени.

3. Адекватность модели, критерии адекватности

Всё то, на что направлено человеческая деятельность называется объектом. Замещение одного объекта другим с целью получения информации о важнейших свойствах оригинала с помощью объекта называется регулированием. В модели должны быть учтены все наиболее существенные факторы, влияющие на процесс, вместе с тем она не должна быть загромождена множеством второстепенных факторов, учёт которых усложнит математический анализ. В зависимости от степени полноты математического описания можно выделить два предельных случая:

• Известна полная система уравнений, описывающая все стороны моделирующего процесса и числовые значения параметров уравнений

• Полное математическое описание отсутствует

Таким образом, можно сделать вывод, что если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, то говорят, что модель адекватна объекту.

С целью построения наиболее адекватной модели в настоящее время получил развитие системный подход.

Индивидуальный подход подразумевает переход от частного к общему и синтезирует систему путем слияния её компонентов.

Системный подход предполагает переход от общего к частному, когда в основе рассмотрения лежит цель, причем исследуемый объект выделяется из окружающей среды. Важным для системного подхода является определение структуры системы – это восстановление совокупностей связей между элементами системы, отражающими их взаимодействие при структурном подходе выявляются состав системы и связи между ними.