6. Взаимное положение прямых линий.

1.         Прямые могут быть пересекаться между собой и тогда точки пересечения их одноименных проекций лежат на одной линии связи (рисунок а).

2.         Прямые могут скрещиваться между собой и тогда точки пересечения их одноименных проекций не лежат на одной линии связи (рисунок б).

3.         Прямые могут быть параллельны между собой и тогда их одноименные проекции также параллельны между собой (рисунок с).

а)                         б)                                  в)

7. Задание плоскости общего и частного положения на чертеже. Положение плоскости относительно плоскостей проекций.

8. Прямая и точка в плоскости.

Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости.

Из элементарной геометрии известно, что прямая принадлежит плоскости, если:

1. oна проходит через две точки, принадлежащие плоскости;

2. oна проходит через 1 точку, принадлежащую плоскости, и параллельна прямой, лежащей в плоскости.

Из первого положения следует, что если прямая принадлежит плоскости, то ее одноименные следы лежат на одноименных следах плоскости.

Рис.1

Рис.2

Пусть следами задана плоскость общего положения Р, построим в этой плоскости прямую l.

9. Главные линии в плоскости.

Главные линии плоскости - это особые прямые, принадлежащие плоскости, позволяющие более точно выявить ориентацию плоскости относи- тельно плоскостей проекций и упростить решение многих задач.      Главными линиями плоскости являются прямые уровня: горизонталь h, фронталь f и профильная р, а также линии наибольшего наклона, при помощи которых можно определить угол наклона плоскости к плоскостям проекций П₁, П₂, П₃. 

Горизонталь, h - это прямая, лежащая в плоскости заданной и параллельная горизонтальной плоскости проекций (рисунки 4 а, б, в).

Фронталь, f – прямая, лежащая в заданной плоскости и параллельная фронтальной плоскости проекций (рисунок 4).

а)                         б)                         в)                г)

Рисунок 4

Линия наибольшего ската, 1-2 (рисунок 4 г) – прямая, принадлежащая заданной плоскости и перпендикулярная к её горизонталям и фронталям. Прямой угол, составленныйл.н.с. плоскости с ее горизонталью, проецируется на горизонтальную плоскость без искажения.

Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.

10. Взаимное положение прямой и плоскости.

Рассмотрим два случая взаимного положения прямой и плоскости: прямая параллельная и перпендикулярная плоскости.

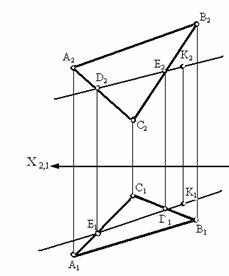
1. Прямая параллельная плоскости.

Прямая параллельна плоскости, если она параллельна прямой b, принадлежащей этой плоскости.

Прямые, параллельные плоскостям, заданным различными способами показаны на рис. 3.8.

2. Прямая перпендикулярная плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости.

Подробно перпендикулярность прямых рассмотрена в лекции № 4.

.

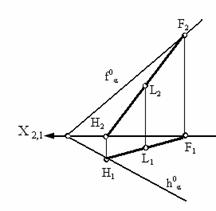
Рис. 3.8. Прямые, параллельные плоскостям, заданным:

а – плоскостью треугольника АВС; б – двумя пересекающимися прямыми а∩b; в – горизонтальным h⁰_α и фронтальным f⁰_α следами