Задание 7 определение усилий в стержнях сложной фермы
Задание состоит в расчете фермы (рис. 7.1), у которой нет ни одного узла, в котором сходятся только два стержня. Метод сечений также не применим, поскольку нельзя провести ни одного сечения, в котором три стержня не пересекаются в одной точке. Поскольку ни одни из перечисленных методов не применим, расчет такой фермы производится методом замены стержней.
Схема фермы показана на рис. 7.1, исходные данные для расчета – в табл. 7.1.
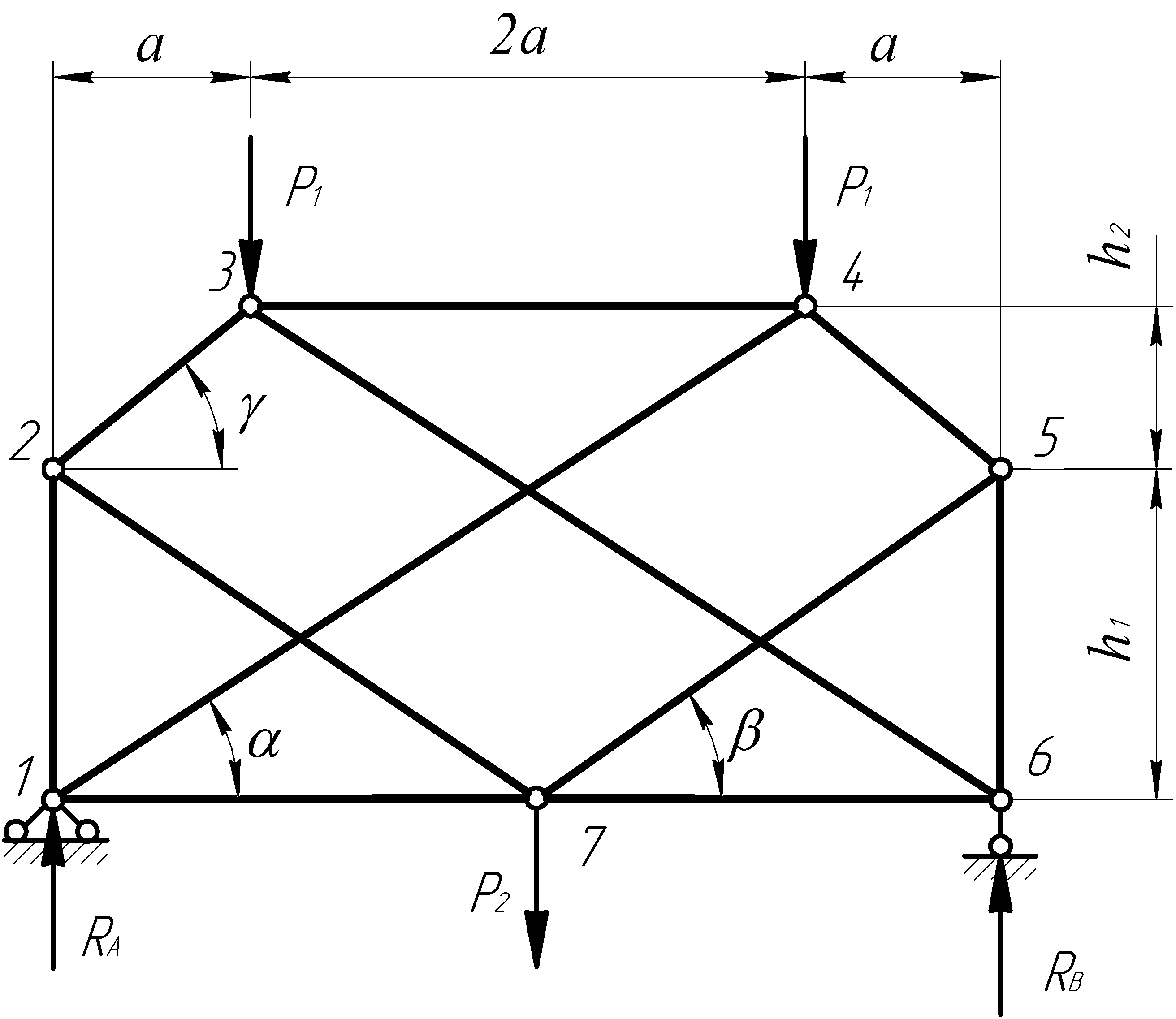
Рисунок 7.1 – Схема к расчету сложной фермы
Таблица 7.1 – Исходные данные к расчету сложной фермы
Вари-ант |
Р1, кН |
Р2, кН |
а, М |
h1, м |
h2, м |
Вари-ант |
Р1, кН |
Р2, кН |
а, М |
h1, м |
h2, м |
1 |
90 |
100 |
2 |
1,5 |
3,07 |
16 |
105 |
80 |
2,7 |
2,26 |
4,53 |
2 |
80 |
90 |
2,5 |
1,88 |
3,77 |
17 |
93 |
73 |
3,0 |
2,5 |
5,03 |
3 |
100 |
90 |
1,8 |
1,36 |
2,71 |
18 |
95 |
78 |
3,1 |
2,6 |
5,2 |
4 |
100 |
110 |
2,6 |
1,96 |
3,91 |
19 |
82 |
100 |
3,2 |
2,68 |
5,37 |
5 |
90 |
100 |
2,5 |
1,89 |
3,77 |
20 |
60 |
93 |
3,0 |
2,5 |
5,03 |
6 |
90 |
80 |
2,2 |
1,66 |
3,31 |
21 |
74 |
92 |
2,8 |
2,36 |
4,7 |
7 |
80 |
60 |
2,5 |
1,88 |
3,77 |
22 |
82 |
105 |
2,9 |
2,4 |
4,8 |
8 |
100 |
50 |
2,8 |
2,11 |
4,22 |
23 |
73 |
96 |
3,3 |
2,67 |
5,34 |
9 |
80 |
50 |
3,0 |
2,34 |
4,68 |
24 |
64 |
82 |
2,6 |
2,1 |
4,2 |
10 |
60 |
120 |
2,75 |
2,15 |
4,29 |
25 |
72 |
100 |
2,5 |
2,0 |
4 |
11 |
75 |
60 |
3,2 |
2,5 |
5,0 |
26 |
58 |
72 |
2,8 |
2,25 |
4,5 |
12 |
75 |
80 |
2,4 |
1,87 |
3,74 |
27 |
64 |
100 |
3,1 |
2,5 |
5,0 |
13 |
70 |
80 |
2,6 |
2,03 |
4,06 |
28 |
76 |
94 |
3,2 |
2,59 |
5,18 |
14 |
60 |
110 |
3,5 |
2,73 |
5,46 |
29 |
82 |
103 |
3,3 |
2,67 |
5,34 |
15 |
110 |
85 |
3,3 |
2,6 |
5,15 |
30 |
68 |
110 |
3,0 |
2,43 |
4,85 |
Порядок решения задачи
Проверить геометрическую неизменяемость фермы.
Определить опорные реакции.
Найти величины углов α и β.
Заменить заданную систему основной (рис.7.2):
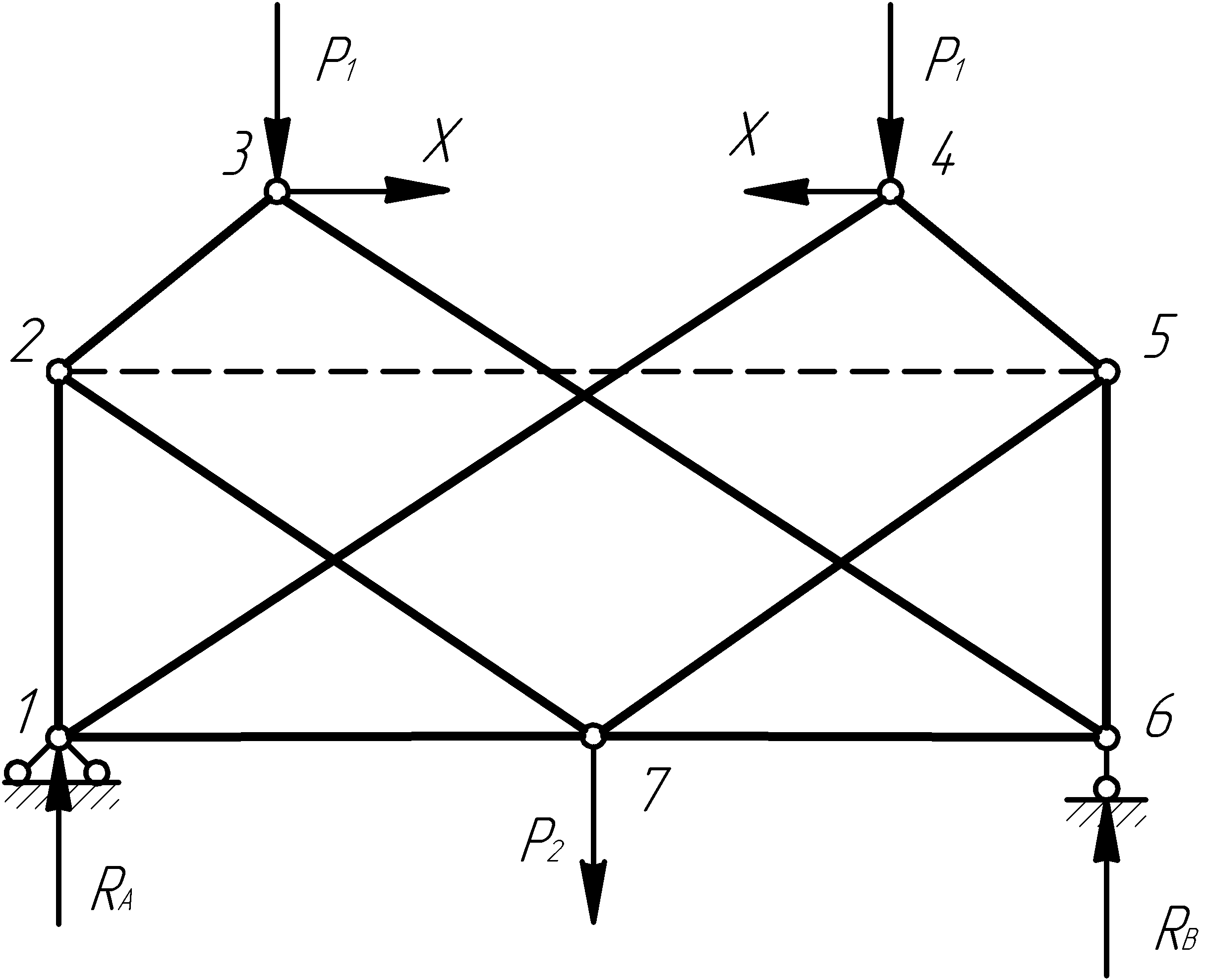
Рисунок 7.2 – Основная система фермы
При замене заданной системы основной системой целесообразно выбросить стержень 3-4 и по его направлению приложить усилие Х. Для обеспечения геометрической неизменяемости фермы необходимо добавить стержень. Заменяющий стержень рекомендуется располагать горизонтально (например, стержень 2-5). Тогда в уравнения равновесия войдет минимальное число тригонометрических функций.
Определить усилия в стержнях основной системы от сил Р1, Р2 и Р3., не учитывая неизвестные силы Х. Обозначить эти усилия как
.
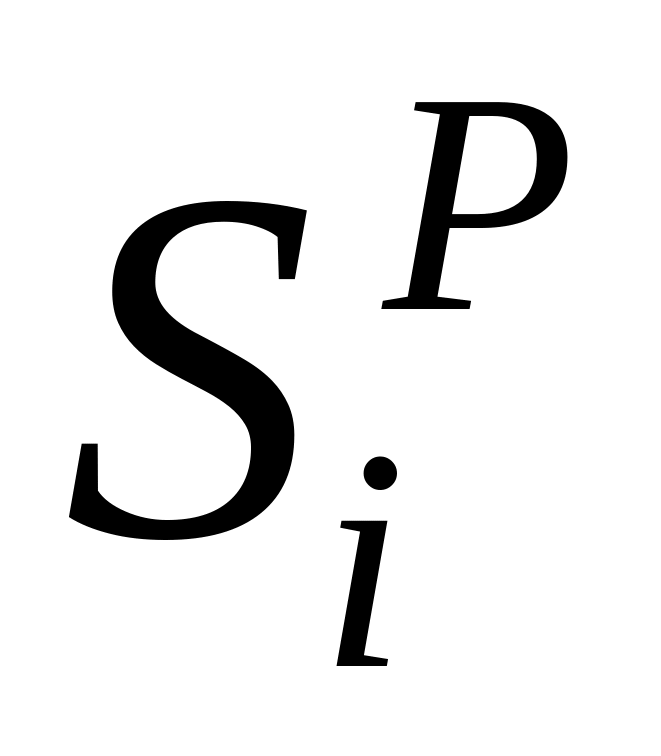Нижний индекс обозначает номер стержня,
верхний индекс показывает, что усилие
определено от внешних сил Рі.
Расчет начинать с узла 3 или 5 методом вырезания узлов. Затем переходить к узлу, в котором сходятся два стержня с неизвестными усилиями.
Рассчитать усилия в стержнях основной системы от сил Х = 1. Расчет начинать с узла 3 или 5 (в которых сходятся всего два стержня). Полученные усилия обозначить как
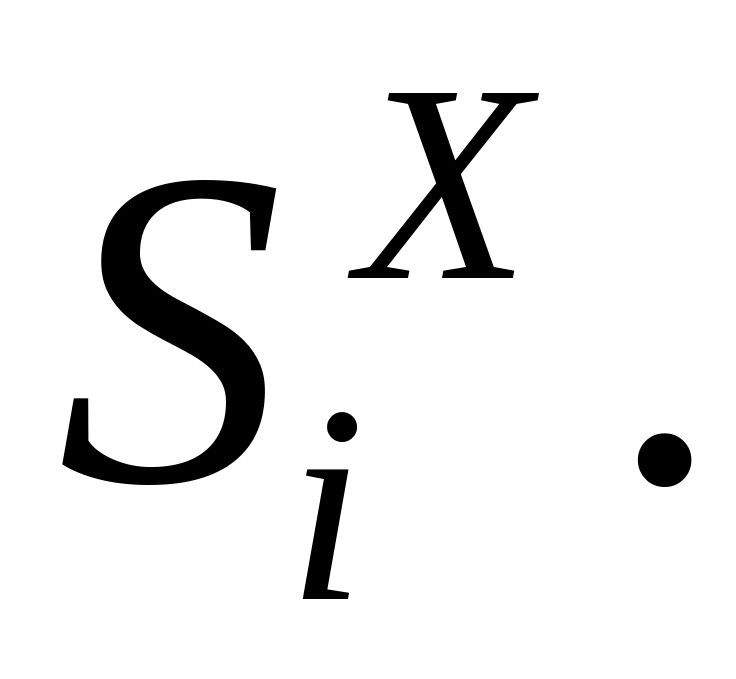
Усилия в любом стержне преобразованной системы определяются по зависимости
(7.1)
Поскольку в исходной ферме стержень 2-5 отсутствует, усилие в нем, рассчитанное по формуле (7.1) должно быть равно нулю:
(7.2)
Из этого условия определяется неизвестная величина Х:
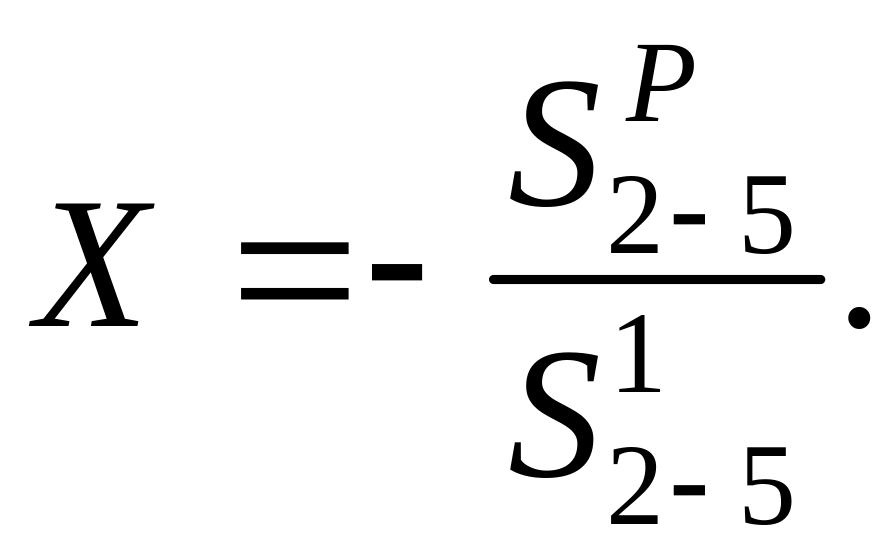7.3)
По зависимости (7.1) определить усилия во всех остальных стержнях фермы. Результаты расчета занести в таблицу 7.2.
Таблица 7.2 – Результаты расчета усилий в стержнях
Номера стержней |
Усилия от нагрузки |
Полное усилие в стержнях фермы |
|
Рі |
Х = 1 |
||
3-4 |
|
|
|
4-5; 3-2 |
|
|
|
5-6; 2-1 |
|
|
|
6-7; 1-7 |
|
|
|
7-5; 7-2 |
|
|
|
6-3; 1-4 |
|
|
|
2-5 |
|
|
|