Приклади розв’язання завдань контрольних робіт

Приклад 1. Знайти область визначення функції .

Розв’язання. Областю визначення є множина точок, для яких виконуються умови: , . Отже, ;

Область визначення – інтервал .

Приклад 2. Дослідити функцію на парність .

Розв’язання.

Функція ні парна, ні непарна.

Приклад 3. Побудувати графік функції .

Розв’язання. Графік функції відомий, це парабола.

Приклад 4. Знайти границю:

1. Щоб розкрити невизначеність виду задана відношенням двох многочленів, треба чисельник і знаменник розділити на найвищий степінь у цих многочленах

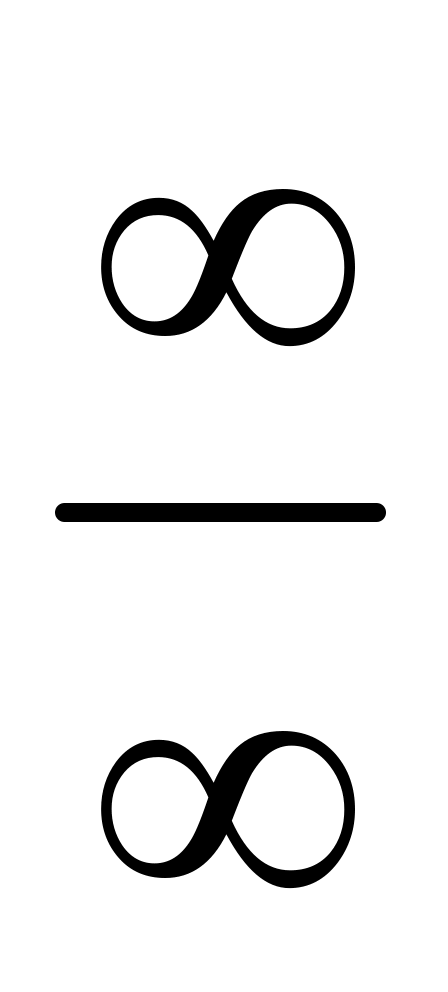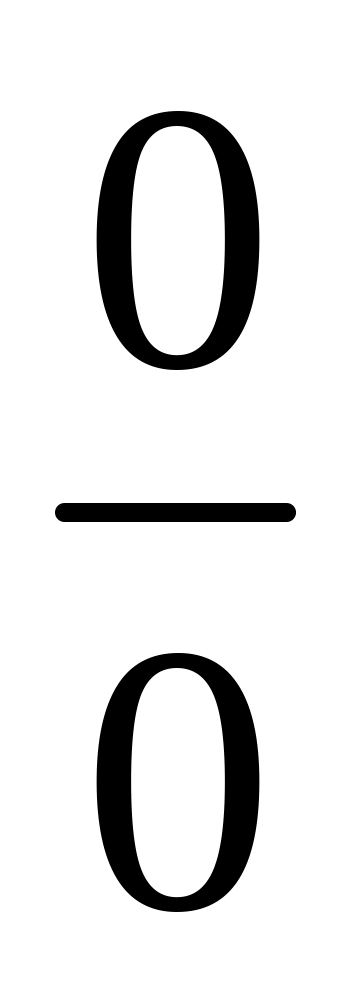2. Щоб розкрити невизначеність виду задана відношенням двох многочленів, треба в чисельнику і знаменнику виділити критичний множник і скоротити на нього

3. Щоб розкрити невизначеність виду задана ірраціональними виразами, необхідно позбутись від ірраціональності, помноживши на спряжений вираз

4. Щоб розкрити невизначеність виду задана ірраціональними виразами необхідно позбутись від ірраціональності, помноживши на спряжений вираз

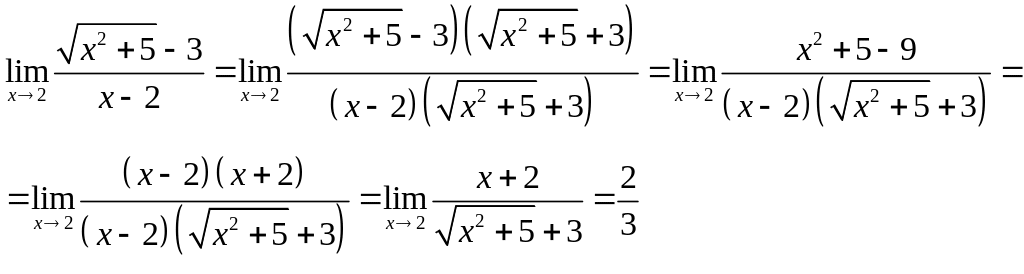
5. Щоб розкрити невизначеність виду задана виразами, що містять тригонометричні функції, застосовують першу важливу границю

6. Щоб розкрити невизначеність виду застосовують другу важливу границю

Приклад 5. Знайти похідну функції, якщо .

Розв’язання. За правилами та формулами диференціювання дістанемо

Приклад 6. Знайти похідну функції, якщо .

Розв’язання.

Приклад 7. Дослідити функцію і побудувати її графік.

Розв’язання.

1. Область існування функції .

2. Графік перетинає вісь абсцис в точці .

3. Функція загального вигляду неперіодична.

4. Функція в точці має розрив другого роду і , отже вісь ординат є вертикальна асимптота.

5. Похідна дорівнює нулю при і не існує при .

Складемо таблицю і визначаємо інтервали монотонності функції.

x		0
y′		не існує	-	0	+
y		не існує

6. Друга похідна всюди, крім точки , де вона не існує. Отже, крива вгнута і точок перегину немає.

7. Знаходимо похилу асимптоту.

,

.

Рівняння похилої асимптоти .

8. Будуємо графік

Приклад 8. Обчислити інтеграл .

Розв’язання. При розв’язанні подібних інтегралів застосовують метод заміни змінної, а саме, введення під знак диференціала. Враховуючи, що , маємо

.

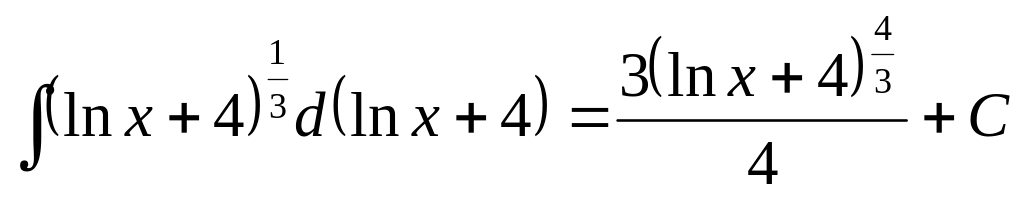Приклад 9. Обчислити інтеграл .

Розв’язання. При розв’язанні подібних інтегралів застосовують метод заміни змінної, а саме, підстановка.

.

Приклад 10. Обчислити інтеграл .

Розв’язання. При розв’язанні подібних інтегралів застосовують метод інтегрування частинами.

.

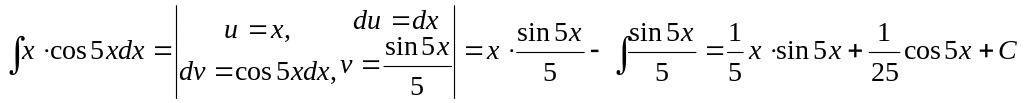Приклад 11. Обчислити інтеграл .

Розв’язання. Підінтегральна функція - правильний дріб, розкладемо на суму елементарних дробів

, де - невизначені коефіцієнти. Звідси

.

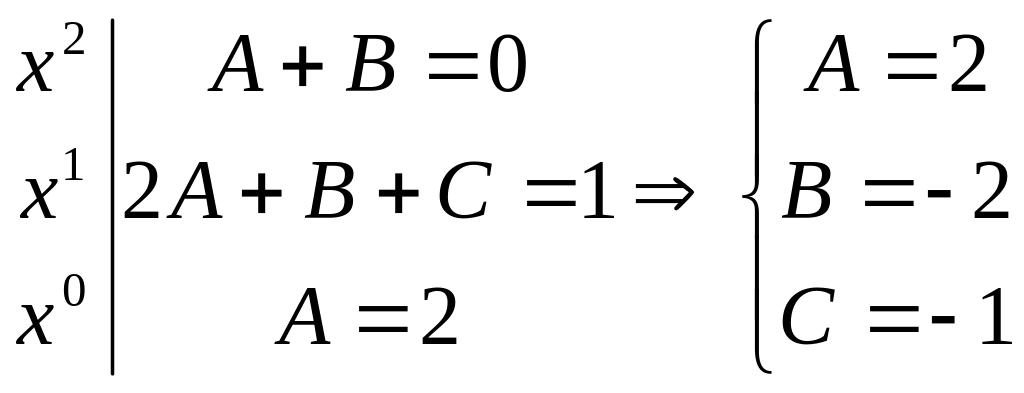Тоді

.

Приклад 12. Обчислити інтеграл .

Розв’язання. Визначені інтеграли обчислюються за формулою Ньютона-Лейбніца.

.

Приклад 13. Обчислити визначник .

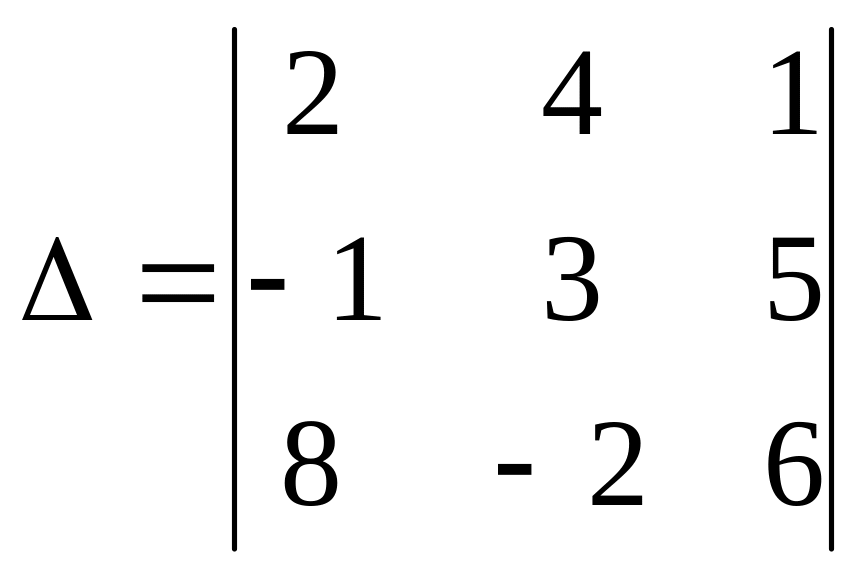Розв’язок.

.

Приклад 14. Знайти обернену матрицю до матриці . Зробити перевірку.

.

Розв’язок. 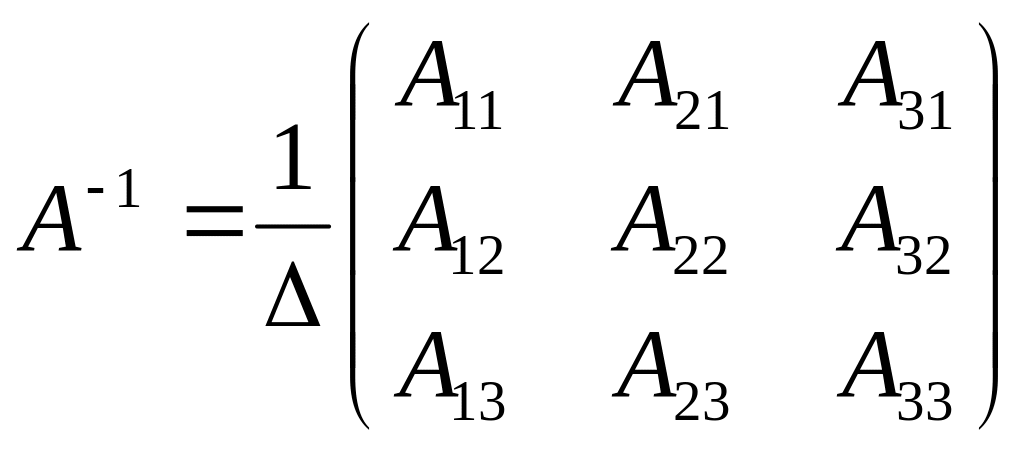, де - алгебраїчні доповнення елементів матриці.

.

.

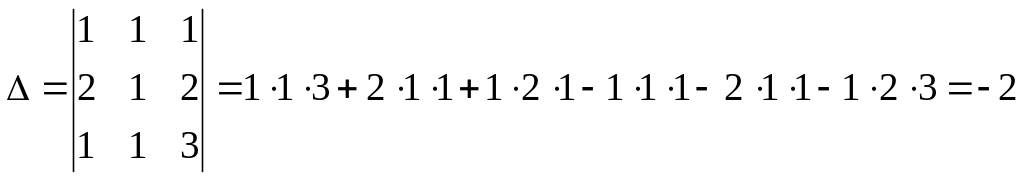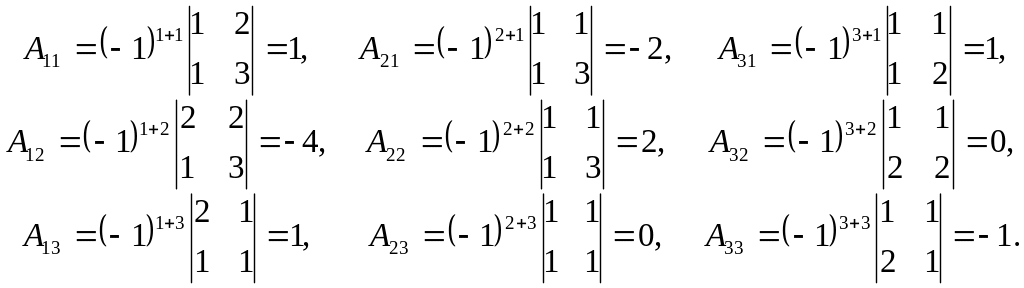
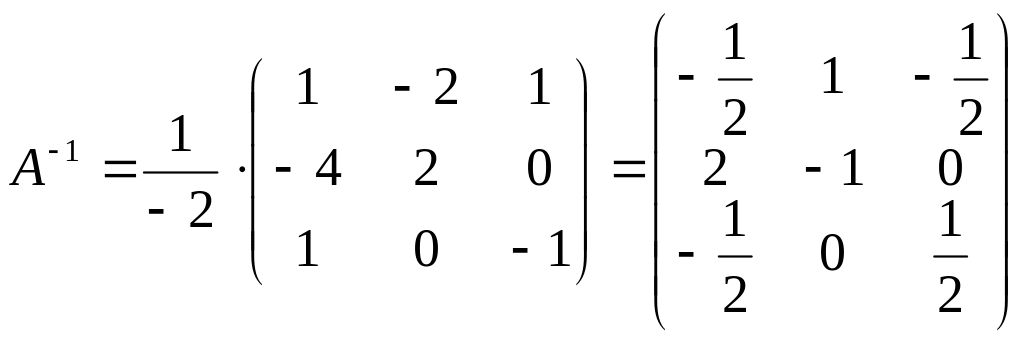Зробимо перевірку .

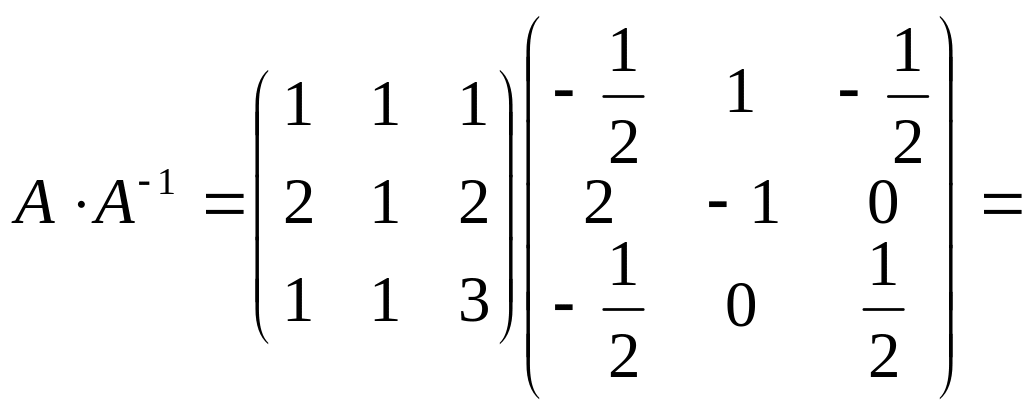
Приклад 15. Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом.

.

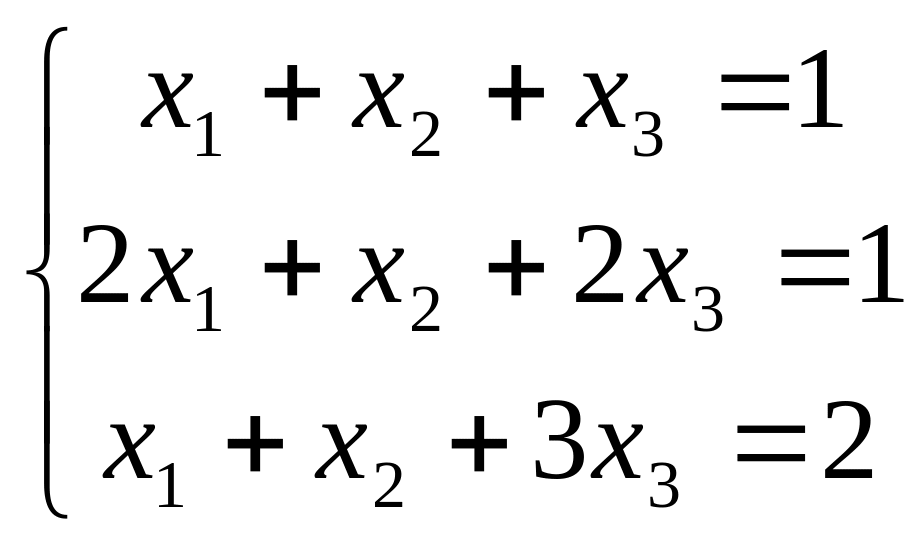Розв’язок.

1). Метод Крамера:

Знайдемо визначник системи 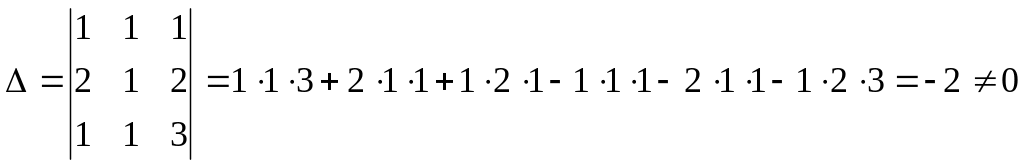, отже система має єдиний розв’язок.

; ; .

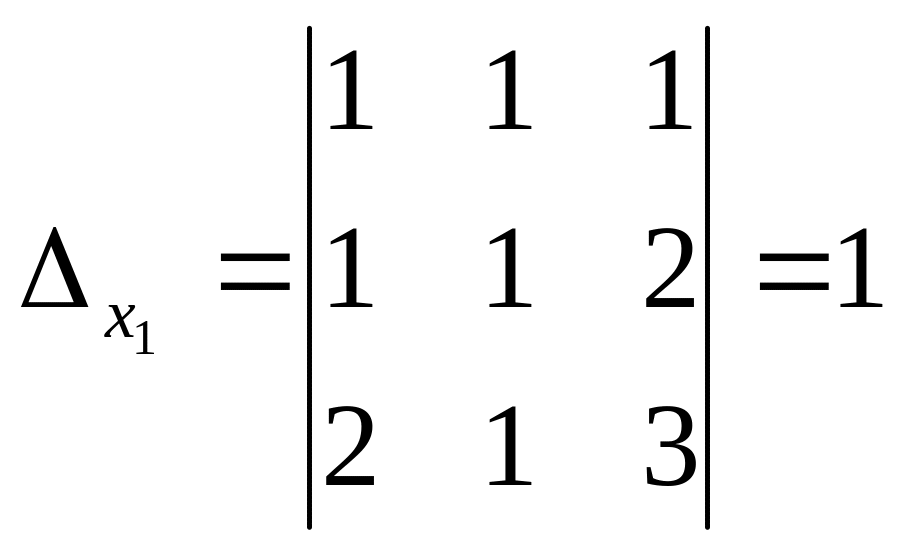За формулами Крамера ; ; .

2). Метод Гауса:

.

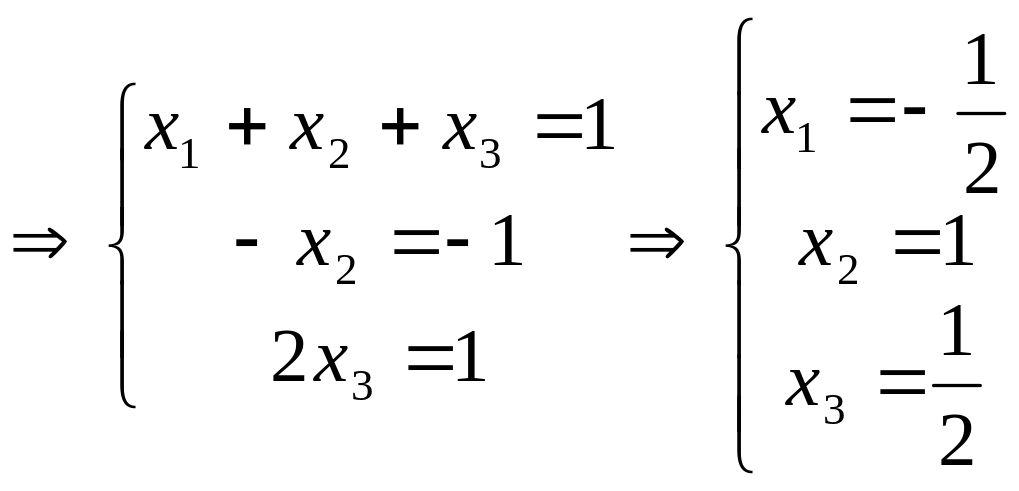3). Матричний метод:

Матриці і нам відомі з умови, необхідно знайти матрицю (з попереднього прикладу нам відома матриця ).

, , , .

,

; ; .

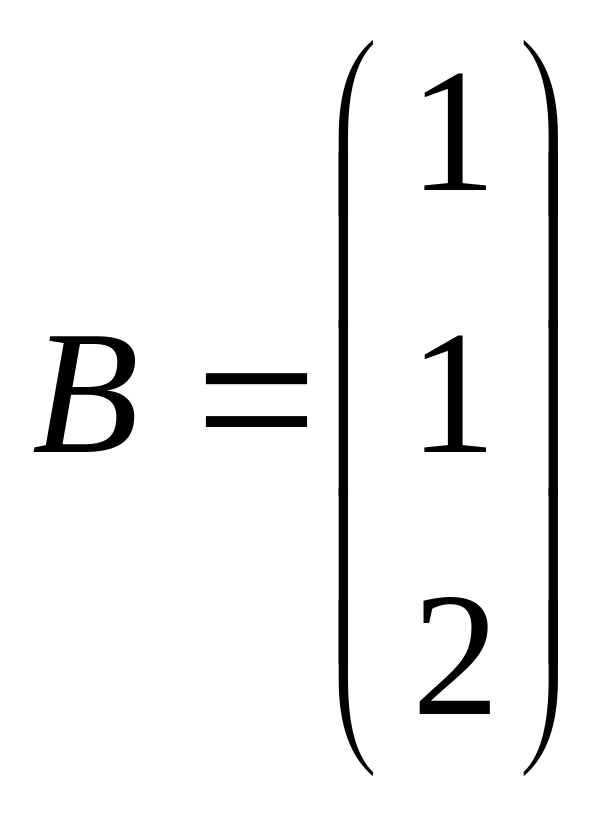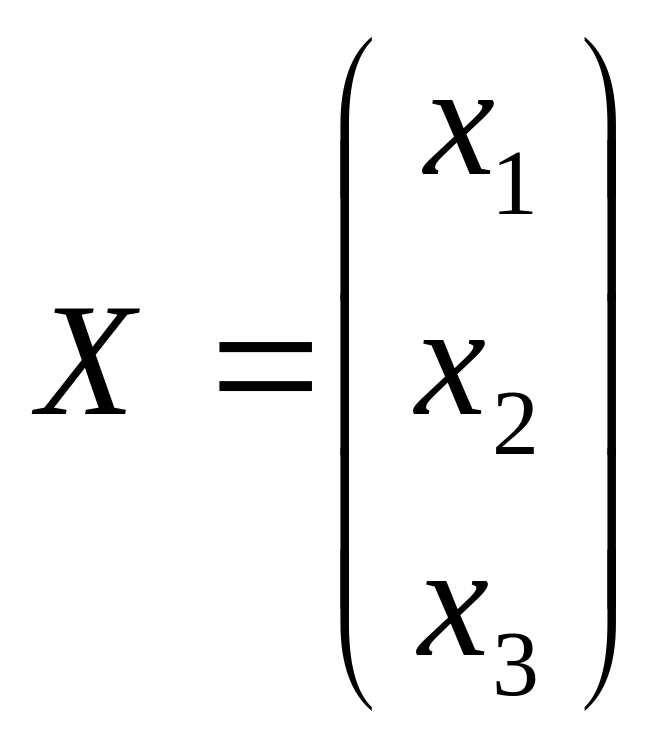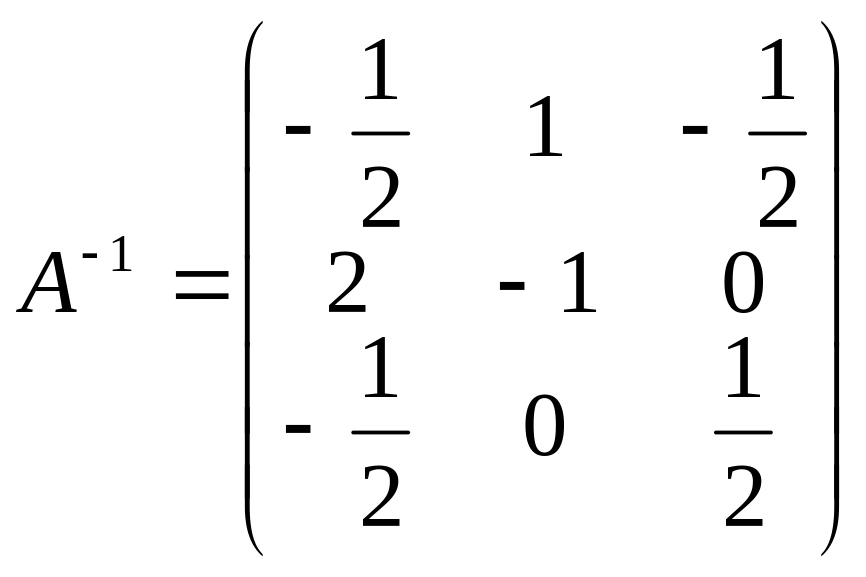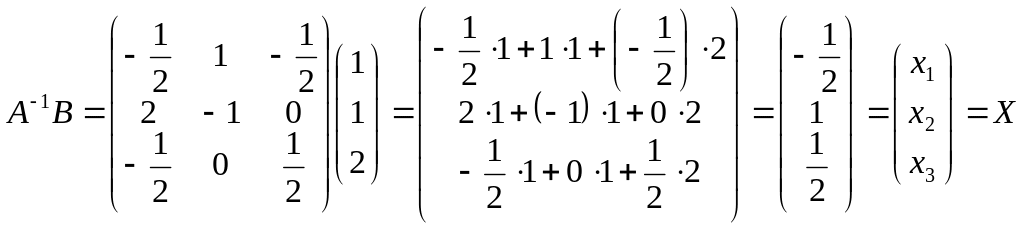Приклад 16. Дослідити систему лінійних рівнянь на сумісність і, якщо це можливо, знайти розв’язки: .

Розв’язок. система лінійних рівнянь – сумісна, бо має розв’язок (3, 1). З’ясуємо, скільки розв’язків має ця система; припустимо, що сукупність чисел є розв’язком цієї системи; тоді

або

підставивши у рівність замість число 3, дістанемо . Отже, розв’язок збігається з розв’язком (3, 1) і дана система має єдиний розв’язок (3, 1), тобто є визначеною системою.

Приклад 17. В трапеції відношення основи до основи дорівнює . Беручи за базис вектори і , знайти координати векторів , , , , , .

Розв’язок. За умовою задачі .

В изначаємо координати векторів:

1) ;

;

4) ;

5) ;

6) .

Приклад 18. Скласти канонічне рівняння прямої, що проходить через дану точку М₀ паралельно вектору якщо

.

Розв’язок. Скористаємося формулою для запису канонічного рівняння прямої .

Маємо .

Приклад 19. Скласти канонічне рівняння еліпса, фокуси лежать на осі ОХ, причому і .

Розв’язок. Оскільки , то , звідки . З рівності визначаємо .

Тоді шукане рівняння еліпса має вигляд .

Приклад 20. Знайти рівняння параболияка має фокус і вершину в початку координат.

Розв’язок. Оскільки фокус лежить на осі під вісю ОХ, то вісь ординат є фокальною віссю параболи, рівняння якої має вигляд . Внаслідок того, що , маємо . Тоді - шукане рівняння параболи , директрисою якої є пряма .

Приклад 21. Знайти загальний інтеграл диференціального рівняння:

.

Розв’язок. Перенесемо все в ліву частину і погрупуємо

Перетворимо ліву частину рівняння

Поділивши обидві частини цього рівняння на функцію , дістанемо рівняння з відокремлюванними змінними

, інтегруючи, яке знаходимо загальний інтеграл

або , звідки

, або .

Рівняння має розв’язки і , тому прямі і є інтегральними кривими данного рівняння. Вони не утворюються із загального інтеграла ні при якому значенні . Отже, розв’язки і є особливими і їх слід виписувати додатково до загального інтеграла.

Приклад 22. Розв’язати рівняння: .

Розв’язок. Для цього рівняння , тому, поклавши , , дістанемо

, ; ;

, сталі і доберемо так, щоб

Розв’язуючи цю систему, знайдемо , тому заміною змінної задане рівняння зводиться до однорідного:

.

За допомогою підстановки знаходимо загальний інтеграл цього рівняння:

Звідси, враховуючи, що , дістанемо загальний інтеграл заданого рівняння

Приклад 23. Знайти розвязок

Розв’язок.

Приклад 24. Проінтегрувати рівняння в повних диференціалах:

Розв’язок. Маємо .

, де - довільна диференційовна функція змінної . Її потрібно підібрати таким чином, щоб виконувалась рівність . Через те, що , матимемо . Звідси , , отже, . Загальний іртеграл рівняння буде .

Приклад 25. Дослідити ряд на збіжність:

Розв’язок. Скористаємося ознакою Д’Аламбера:

, за умовою , тоді .

Отже 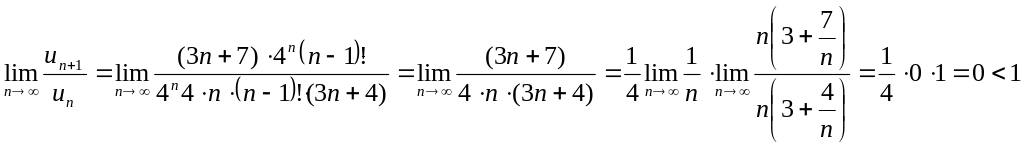заданий ряд збіжний.

Приклад 26. Дослідити ряд на збіжність: .

Розв’язок. Скористаємося ознакою Коші:

заданий ряд збіжний.