1.3. Решение задач линейного программирования графическим методом

Рассмотрим задачу линейного программирования с ограничениями-неравенствами, которые имеют вид:

a₁₁x₁ + a₁₂x_{2 +} … + a_1nx_n ≥ b₁;

a₂₁x₁ + a₂₂x_{2 +} … + a_2nx_n ≥ b₂; (1.3.1.)

………………………………

а_m1x₁ + a_m2x_{2 +} … + a_mnx_n ≥ b_m;

и являются линейно-независимыми. Последнее означает, никакое из них нельзя представить в виде линейной комбинации других. Требуется найти x_i ≥ 0, которые удовлетворяют неравенствам и обращают в минимум

L=

Введём уравнения:

=

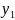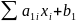
= (1.3.2)

=

где  y_1, y_{2, …,} y_n - добавочные переменные, которые также как и 

x_{1 ,} x_{2, …,} x_n  являются неотрицательными.

Таким образом, имеем общую задачу линейного программирования - найти неотрицательные x_{1 ,} x_{2, …,} x_n y_1, y_{2, …,} y_n, чтобы они удовлетворяли системе уравнений (1.3.2.) и обращали в минимум L=

Коэффициенты в формуле (1.3.2.) перед y_j равны нулю.

Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и Целевую Функцию задачи.

Каждое из неравенств задачи линейного программирования (1.3.1.) определяет на координатной плоскости (x₁Ox₂) некоторую полуплоскость (рис.1.3.1), а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи (1.3.1.) ОДР является пустым множеством.

Все вышесказанное относится и к случаю, когда система ограничений (1.3.1.) включает равенства, поскольку любое равенство

a_i1x₁ + a_i2x₂ = b_i можно представить в виде системы двух неравенств (см. рис.1.3.1)

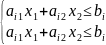(1.3.3.)

ЦФ L(x)=c₁x₁+c₂x₂  при фиксированном значении L(x)=L определяет на плоскости прямую линию c₁x₁+c₂x₂=L  . Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.

Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси Ox₂ (начальная ордината), а угловой коэффициент прямой tg 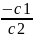   останется постоянным (см.рис. 1.3.1). Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.

Вектор 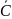  = (c_1, c₂) координатами из коэффициентов ЦФ при x₁ и x₂ перпендикулярен к каждой из линий уровня (см. рис.1.3.1). Направление вектора   совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора  .

Суть графического метода заключается в следующем. По направлению (против направления) вектора   в ОДР производится поиск оптимальной точки  x^* = (x₁^* , x₂^*). Оптимальной считается точка, через которую проходит линия уровня L_max(L_min), соответствующая наибольшему (наименьшему) значению функции L(x). Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.

При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений – единственная точка; задача не имеет решений.

 

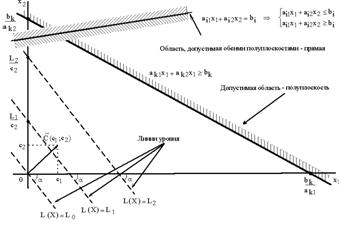
Рисунок 1.3.1 Геометрическая интерпретация ограничений и ЦФ задачи.

Задача №1.

Пример решения задач линейного программирования симплекс–методом.*

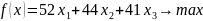
Решение.

Приводим задачу к каноническому виду. Для этого в левую часть правого ограничения вводим дополнительные переменные Х4 , Х5 и Х6 с коэффициентом +1. В целевую функцию переменные Х4 , Х5 и Х6 входят с коэффициентом 0.

Получим:

Находим начальное опорное решение. Для этого свободные переменные приравниваем к 0.

Получаем опорное решение.

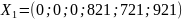
С единичным базисом Б1.

Вычисляем оценки разложения векторов условий по базису опорного решения по формуле.

:

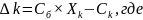Сб = (с1, с2, ... , сm ) — вектор коэффициентов целевой функции при базисных переменных

Xk = (x1k, x2k, ... , xmk ) — вектор разложения соответствующего вектора Аk по базису опорного решения

Сk — коэффициент целевой функции при переменной хk.

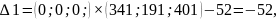
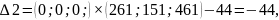
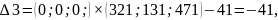
Оценки векторов входящих в базис всегда равны нулю. Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу:

					52		44		41		0		0		0
Б	Сб		А0		А1		А2		А3		А4		А5		А6		D1
A4	0		821		341		261		321		1		0		0		2.4
A5	0		721		191		151		131		0		1		0		4
A6	0		921		401		461		471		0		0		1		2.3
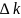
		0		-52		-44		-41		0		0		0

Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце "Б" записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов соответствует номерам разрешенных неизвестных в уравнениях ограничениях. Во втором столбце таблицы "Сб" записываются коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце "Сб" оценки единичных векторов, входящих в базис, всегда равных нулю.

В последней строке таблицы с оценками Δk в столбце "А0" записываются значения целевой функции на опорном решении Z(X1).

Начальное опорное решение не является оптимальным, так как в задаче на максимум оценки Δ1 = -52, Δ2= -44, Δ3= -41 для векторов А1, А2 и А3 отрицательные.

По теореме об улучшении опорного решения, если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше.

Определим, введение какого из двух векторов приведет к большему приращению целевой функции.

Приращение функции находится по формуле:

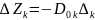
Вычислим значение D по формуле:

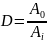
Полученные значения записываем в таблицу.

Находим приращение целевой функции при введении в базис первого вектора

Следовательно, для более быстрого приближения к оптимальному решению необходимо ввести в базис опорного решения вектор А1 вместо первого вектора базиса А6, так как минимум параметра D01 достигается в третьей строке .

Производим преобразование Жордана с элементом Х31 =401 , получаем второе опорное решение Х2 = (2.3;0;0;36.7;281.7;0) с базисом Б2 = (А4, А5, А1).

			52	44	41	0	0	0
Б	Сб	А0	А1	А2	А3	А4	А5	А6
A4	0	36.7	0	-131.15	-81.38	1	0	-0.85
A5	0	281.7	0	-68.65	-94.38	0	1	-0.478
A1	52	2.3	1	1.15	1.18	0	0	0.0025
		119.6	0	15.8	20.36	0	0	0.13

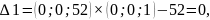
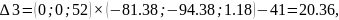
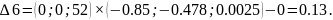
Это решение является единственным оптимальным, так как для всех векторов, не входящих в базис оценки положительные

Δ2 = 15.8, Δ3 = 20.36, Δ6 = 0.13.

Ответ: max f(X)=119.6 при Х=(2.3;0;0;36.7;281.7;0)