Отношения между суждениями

В повседневной деятельности человек сталкивается с различными мнениями, суждениями, которые необходимо сравнивать и определять их совместимость. Для верного анализа высказываний надо иметь четкое представление о тех отношениях, в которых могут находиться между собой суждения. Основу отношений между суждениями составляет их сходство по содержанию, выражаемое в таких логических характеристиках, как смысл и истинность суждений. В соответствии с этим логические отношения устанавливаются не между любыми, а лишь между сравнимыми суждениями, т.е. теми, которые имеют общий смысл. Рассмотрим отношения между простыми суждениями, а затем - между сложными.

Сравнимыми среди простых суждений являются суждения, имеющие одинаковые термины и различающиеся по качеству или количеству. Несравнимыми среди простых суждений являются такие, которые имеют различные субъекты или предикаты.

Сравнимые суждения делятся на совместимые и несовместимые. Совместимыми являются суждения, которые одновременно могут быть истинными.

О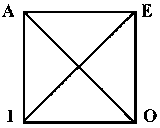 тношения между простыми суждениями обычно иллюстрируют с помощью схемы, получившей название логического квадрата. Логический квадрат (квадрат противоположностей) - это диаграмма, служащая для мнемонического запоминания логических отношений между видами суждений по объединенной классификации.

Вершины квадрата обозначают вид суждения по объединенной классификации: А, Е, 0, I. Стороны и диагонали символизируют логические отношения между простыми суждениями (кроме эквивалентных). Верхняя сторона есть О отношение А и Е - противоположность (контрарность); нижняя сторона - отношение между I и O - частичная совместимость (субконтрарность);две вертикальные стороны - отношения между А и I (левая), Е и О (правая) - подчинение; диагонали - отношения между А и О, Е и I – противоречие (контрадикторность).

Отношения между суждениями можно записать в виде таблицы, где И – истинность, Л – ложность, ∞ - неопределенность, таким образом, если Аи, то Ел, Iи, Ол…

	А	Е	I	О
А истинно	----	Л	И	Л
А ложно	----	∞	∞	И
Е истинно	Л	----	Л	И
Е ложно	∞	----	И	∞
I истинно	∞	Л	----	∞
I ложно	Л	И	----	И
O истинно	Л	∞	∞	----
О ложно	И	Л	И	----

Перейдем к рассмотрению отношений между сложными суждениями.

Сравнимые среди сложных - это суждения, которые имеют одинаковые составляющие и различаются типами логических связок, включая отрицание: например, "Норвегия или Швеция являются членами НАТО" и "Неверно, что Норвегия и Швеция являются членами НАТО". Сравнивать эти суждения можно потому, что у них общие составляющие, хотя по логической форме они отличаются друг от друга: первое из них дизъюнктивное суждение, второе - отрицание конъюнкции. Наличие общих составляющих позволяет сопоставлять их по смыслу и установить зависимости по истинности. Несравнимыми среди сложных суждений являются суждения, которые частично или полностью различаются составляющими их суждениями. Например, нельзя сравнивать следующие два суждения: "Слух обо мне пройдет по всей Руси великой, и назовет меня всяк сущий в ней язык, и гордый внук славян, и финн, и ныне дикой тунгус, и друг степей калмык" и "Чем дальше в лес, тем больше дров". Различия в составляющих не позволяют установить смысловую и истинную зависимость между суждениями.

Между сложными суждениями складываются такие же виды отношений, как и между простыми. Характер этих отношений можно определить с помощью таблиц истинности.

Для использования табличного метода определения истинности необходимо знать определения основных логических связок.

Чтобы построить таблицу истинности, нужно сначала, считая, что все простые суждения независимы друг от друга, перебрать все возможные сочетания их значений. Таких сочетаний будет – 2n, где n – число различных простых суждений в составе сложного суждения.

Для всех типов отношений между сложными суждениями можно построить следующую таблицу, где р и q – простые суждения в составе сложного, Λ - знак конъюнкции, V – знак слабой дизъюнкции, V – знак сильной дизъюнкции, знак импликации →, эквиваленция обозначается знаком ↔.

p	q	pΛq	pVq	PVq	p→q	p↔q
и	и	и	и	л	и	и
и	л	л	и	и	л	л
л	и	л	и	и	и	л
л	л	л	л	л	и	и

Отметим, что конъюнкция истинна, только если оба члена конъюнкции истинны, сильная дизъюнкция истинна, когда истинным является лишь один из членов дизъюнкции.

«Студенты НТУ «ХПИ» обучаются или стационарно, или заочно, или на вечернем отделении» – это сложное дизъюнктивное суждение, состоящее из 3-х простых, его логическая форма (pVqVr), где p,q,r - простые суждения в составе сложного (p – «Студенты НТУ «ХПИ» обучаются стационарно», q- «Студенты НТУ «ХПИ» обучаются зачно», r - «Студенты НТУ «ХПИ» обучаются на вечернем отделении») Построим таблицу истинности и заполним ее, помня о том, что сильная дизъюнкция истинна, лишь когда ОДИН из членов дизъюнкции истинен.

p	q	r	pVqVr	(p↔q)	(p‾ → r)	(p↔q) Λ(p‾ → r)
и	и	и	л	и	л	л
и	и	л	л	и	и	и
и	л	и	л	л	л	л
и	л	л	и	л	и	л
л	и	и	л	л	и	л
л	и	л	и	л	л	л
л	л	и	и	и	и	и
л	л	л	л	и	л	л

Рассмотрим другой пример: «Если я сделаю контрольную работу по логике, то тогда и только тогда я получу допуск к экзамену, а если я не сделаю контрольную работу по логике, то у меня будет свободное время». Это суждение можно записать в виде формулы (p↔q) Λ(p‾ → r), где p, q, r - простые суждения в составе сложного, ‾ - знак отрицания. Преобразованное суждение можно представить так: «Если я сделаю контрольную работу по логике(p), то тогда и только тогда я получу возможность сдавать зачет(q), и если я не сделаю контрольную работу по логике (p‾), то у меня будет свободное время (r)». Заполним далее построенную таблицу истинности. Чтобы определить, в каких случаях это суждение истинно, мы должны 1. понять, в каких случаях истинно выражение (p↔q), 2. понять, в каких случаях истинно выражение (p‾ → r), помня о том, что если р истинно, то не-р – ложно, 3. определить истинность всего суждения, помня, что конъюнкция истинна, лишь когда оба члена конъюнкции истинны.