8.3. Погрешности средств измерений

В результате воздействия большого числа случайных и детерми­нированных факторов, возникающих в процессе изготовления, хра­нения и эксплуатации измерительных средств, номинальные значе­ния мер и показания измерительных приборов отличаются от истин­ных значений измеряемых величин. Эти отклонения характеризуют погрешности измерительных средств.

Под абсолютной погрешностью меры понимается алгебраическая разность между ее номинальным х„ и действительным X значениями.

Под абсолютной погрешностью Дх измерительного прибора пони­мается алгебраическая разность между показанием прибора и дей­ствительным значением измеряемой величины.

Погрешность меры определяется по формуле , а погрешность измерительного прибора из аналогичного выра­жения

Степени точности средства измерений характеризует относитель­ная погрешность, т. е. выраженное в процентах отношение абсо­лютной погрешности к действительному значению измеряемой или воспроизводимой данным средством измерений величины:

В эту формулу вместо х, можно подставить номинальное значе­ние меры или показание измерительного прибора (8«1).

Если диапазон измерения прибора включает и нулевое значение измеряемой величины, то относительная погрешность обращается в бесконечность в нулевой точке шкалы. В этом случае пользуются понятием приведенной погрешности, равной отношению абсолютной погрешности измерения измерительного прибора к некоторому нор­мирующему значению :

В качестве нормирующего значения применяется значение, ха­рактерное для данного вида измерительного прибора. Это может быть, например, диапазон измерений, верхний предел измерений, длина шкалы и т. п. Важной характеристикой измерительного прибора является по­рог реагирования (чувствительности).

Под порогом реагирования понимается изменение измеряемой ве­личины, вызывающее наименьшее изменение показаний измеритель­ного прибора, которое еще может быть обнаружено наблюдателем при нормальном для данного прибора способе отсчета показаний.

При измерении переменных во времени величин большое значение приобретает анализ динамических погрешностей, которые ис­кажают частотный спектр измеряемой функции.

8.4. Нормирование погрешностей средств измерений

Государственными стандартами на отдельные виды средств из­мерений устанавливаются нормы на значения их суммарных по­грешностей и отдельных составляющих, таких, как вариация пока­заний, непостоянство показаний, погрешность обратного хода и др.

Значения суммарных погрешностей устанавливаются отдельно для нормальных условий применения средств измерений и для слу­чая отклонения влияющих величин от значений, имеющих место н нормальных условиях.

Под нормальными условиями понимаются такие условия при­менения средств измерения, при которых влияющие на процесс из­мерения величины (температура, влажность, частота и напряжение питания, внешние магнитные поля, положение средств измерения в пространстве и т. д.) имеют нормальные значения или находятся в нормальной области значений. Нормальные значения влияющих величин указываются в стандартах или технических условиях на сред­ства измерений данного вида в форме номиналов с нормированны­ми отклонениями, например температура должна составлять 20 ± 2°С, напряжение питания 220 ± 10 %. Иногда вместо нормальных значе­ний влияющих величин указывают нормальную область их значе­ний (влажность 30—80 %).

Погрешность, свойственная средству измерений, находящемуся в нормальных условиях применения, называется основной погрешно­стью. Основная погрешность средств измерений нормируется пу­тем задания пределов допускаемой основной погрешности. Только в том случае, когда основная погрешность находится в этих пределах, средства измерения допускаются к применению пределы допускаемой основной погрешности мер задаются в виде абсолютных, приведенных или относительных погрешностей. Основная погрешность отдельных однозначных мер задается одно­членной формулой, определяющей пределы допускаемой абсолютной

или относительной основной погрешности

где — предел допускаемой основной абсолютной погрешности; — предел допускаемой относительной основной погрешности; — номинальное значение меры.

Для тех мер, которые не имеют номинального значения, норми­руется не основная погрешность, а допустимый диапазон действи­тельных значений мер.

Основная погрешность отдельных многозначных мер выражается так­же одночленной формулой, определяющей приведенную погрешность:

где Д — диапазон значений воспроизводимой многозначной мерой величины.

Для нормирования пределов допускаемой основной погрешнос­ти наборов и магазинов мер одночленные формулы не применяют­ся, поскольку они не отражают имеющей место зависимости абсо­лютной или относительной погрешности меры от номинального значения воспроизводимой величины. Поэтому для них использу­ются двучленные формулы:

• для абсолютной погрешности

~ для относительной основной погрешности

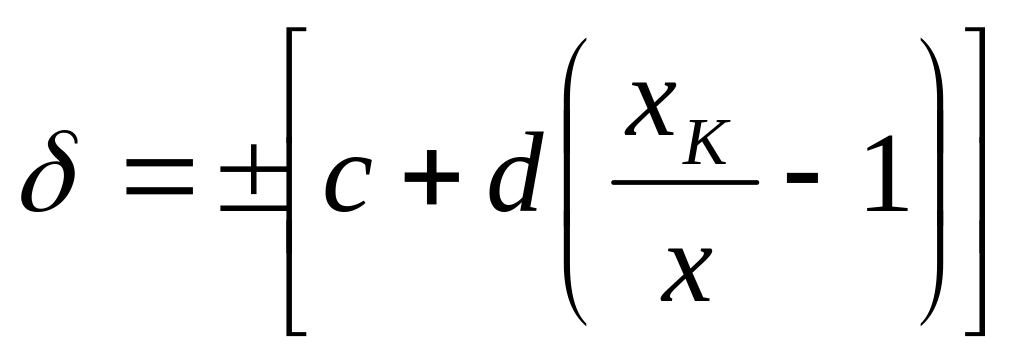
где а, Ь, с, d — постоянные числа; — наибольшее значение вос­производимой данным набором или магазином величины. При предел допускаемой относительной основной по­грешности достигает значения , а при остается всюду больше этой величины. Допускается также использование формулы

где х' — значение воспроизводимой набором или магазином вели­чины, при котором предел допускаемой основной погрешности до­стигает наименьшего значения.

Если зависимость основной погрешности от номинальных зна­чений мер оказывается более сложной, то основная погрешность задается в виде таблицы пределов допускаемой абсолютной основ­ной погрешности для различных номинальных значений мер (на­пример, для мер массы — гирь).

Способ задания пределов допускаемой основной погрешности измерительных преобразователей и приборов определяется главным образом зависимостью погрешности от измеряемой или соответствен­но входной величины