5.3. Моменты случайных величин

Для исследования распределений случайных величин в математической статистике пользуются моментами. Моменты представляют собой систему численных характеристик распределения, вклю-1 чающую среднюю арифметическую и дисперсию.

Моментом ряда распределения (или просто моментом)

относительного начального значения х=а называется сумма произведений от­клонений значений х, от а в степени r на соответствующую частоту

(5,15)

Давая показателю степени г различные значения (г = 0, 1, 2, 3 и т. д.), получим моменты нулевого, первого, второго и т. д. порядка отно­сительно начала. Различают начальные и центральные моменты r -го порядка. Если а = 0, то момент называется начальным. Обозначим на­чальный момент r -го порядка через тогда

(5,16)

Если а - X , то момент называется центральным. Обозначим его через , тогда центральный момент r -го порядка

(5,17)

Обычно для практических целей ограничиваются вычислением моментов не выше четвертого порядка.

Среднее арифметическое значение случайной величины X пред­ставляет собой начальный момент первого порядка

(5,18)

Центральные моменты выражаются через начальные моменты следующим образом:

(5,19)

(5,20)

(5,21)

(5,22)

(5,23)

Центральный момент второго порядка представляет собой дис­персию случайной величины X:

(5,24)

Для распределений случайных дискретных величин:

(5,25)

(5,26)

Для распределения случайных непрерывных величин:

(5,27)

(5,28)

5.4. Асимметрия и эксцесс

Кроме рассмотренных числовых характеристик применяется и ряд других вероятностных характеристик, каждая из которых опи­сывает определенное свойство распределения.

Так, третий центральный момент ^ характеризует степень асим­метрии кривой распределения относительно математического ожи­дания, но для удобства за характеристику асимметрии принимают без­размерную величину, называемую коэффициентом асимметрии а:

(5,29)

При одномодальном распределении асимметрия положительна (a>Q), если мода (х) находится влево от среднего значения М(х), и отрицательная (аг<0), если мода (х) находится вправо от среднего значения М(х) (рис. 5.4). При симметричном распределении =0.

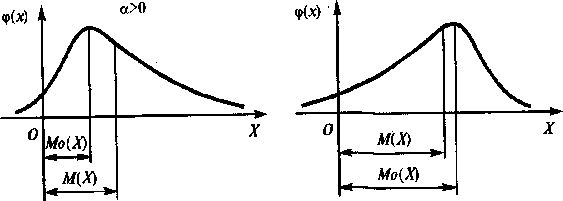
Рис. 5.4. Распределение плотности вероятности при различных значениях коэффициента асимметрии

Четвертый центральный момент ju_t определяет свойство остро­вершинности кривой распределения. -За характеристику этого свой­ства принимают безразмерную величину т, называемую коэффици­ентом эксцесса

(5,30)

При симметричном одномодальном распределении эксцесс обычно положителен (т>0), если кривая распределения островершинна, и отрицателен (г<0), если кривая распределения плосковершинна.

По величине коэффициентов асимметрии и эксцесса можно сде­лать допущение, например, о нормальности распределения изучае­мой случайной величины, хотя это требует более строгой проверки. Для нормального распределения коэффициенты асимметрии и экс­цесса равны нулю (рис. 5.5).

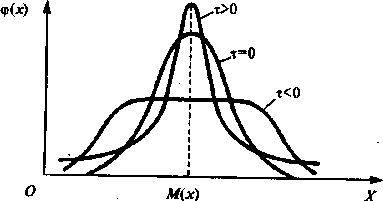
Рис. 5.S. Распределение плотности вероятности с различными коэффициентами эксцесса