11.А и В – матрицы. Чему равно (АВ)т
Свойства транспонированной матрицы
Если матрица A имеет размер n×m, то транспонированная матрица AT имеет размер m×n;
(AT)T = A;
(k · A)T = k · AT; (A + B)T = AT + BT; (A · B)T = BT · AT.
12.Какие преобразования называют элементарными преобразованиями матриц?
Элементарные преобразования матрицы — это такие преобразования матрицы, в
результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования НЕ изменяют множество решений системы линейных алгебраических уравнений, которую представляет собой эта матрица.
Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Элементарными преобразованиями матриц называются следующие преобразования:
1)умножение строки или столбца матрицы на ненулевое число;
2)перестановка местами двух строк или столбцов матрицы;
3)прибавление к некоторой строке матрицы другой ее строки, предварительно умноженной на произвольный коэффициент (некоторое ненулевое число) или прибавление к некоторому столбцу матрицы другого ее столбца, предварительно умноженного на произвольный коэффициент (некоторое ненулевое число).
Если от матрицы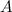 
к матрице 
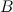перешли с помощью элементарных преобразований, то такие матрицы называют эквивалентными и обозначают 
!Для понимания – это те же действия, которые мы можем делать над уравнениями из системы линейных уравнений, не изменяя множество их корней (решений)
Каждое из элем. Преобразований можно представить как умножение исходной
матрицы на матрицу специального вида, причём, если преобразование нужно над строчками, то специальная матрица слева от исходной, а если над столбцами – то справа.
Специальная матрица – это единичная матрица, над которой проведено требуемое преобразование.
То есть, для умножения і-той строки исходной матрицы на число k ее надо
умножить слева на единичную матрицу, у которой в элементе іі на главной диагонали единица умножена на k (заменена на k). Если умножать на такую матрицу справа – на k умножится і-тый солбец исходной матрицы.
Видео с объяснением и примером: https://www.youtube.com/watch?v=UlsZV9U2iAA
Элементарные преобразованиями матриц нужны для упрощения матриц и приведения их к треугольному виду, который позволяет легче вычислять их определитель.
ПЕРЕСТАНОВКИ, ПОДСТАНОВКИ, ТРАНСПОЗИЦИИ:
http://www.algebraical.info/doku.php?id=glossary:group:permutation
нужные термины по теме
* Биективность. Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Поэтому биективное
отображение называют ещё взаимно-однозначным отображением (соответствием) ..
В случае подстановок биективность означает, что при записи подстановки в виде таблицы из двух строк все элементы в нижней строке (строке образов) различны (инъективность), и в строке образов присутствуют все элементы Xn (сюръективность).
* Инъективность Инъекция в математике (или вложение, или однооднозначным отображение в множество Y) — отображение f множества X в множество Y (f:X→Y), при
котором разные элементы множества X переводятся в разные элементы множества Y, то есть, если два образа при отображении совпадают, то совпадают и прообразы:
f(x)=f(y) => x=y
* Сюръективность – Сюръекция (буквально НАложение, в отличие от
Вложения/инъекции) — отображение множества X |
|
множество Y (f:X→Y), при котором |
||||
на |
||||||
|
|
2 |
|
|
бы одного элемента множества X, то |
|
каждый элемент множества Y является образом хотя |
||||||
есть |
y Y x |
X : y = f (x). |
||||
|
Примеры: |
f:R→R+,F(X)=X2 — сюръективно. |
||||
|
f:R→R,f(x)=x |
|
— не сюръективно (например, не существует x Є R, чтобы f(x)=−9). |
|||
Отображе́ние = Фу́нкция = Опера́тор = Преобразова́ние – соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного
множества ставится в соответствие некоторый элемент из другого множества.
ВНИМАНИЕ! В некоторых учебниках перестановка и подстановка называются наоборот или вообще обе сущности называют перестановкой, т.к. по сути подстановка основана на перестановках и в англоязычной литературе это всё permutation. Из-за этого возможна путаница в терминах. Ниже – так, как у вас в конспектах.
13.Что такое подстановка?
Подстановка – взаимно-однозначное (=биективное*) отображение* конечного
множества Е на себя.
Подстановка конечного множества первых n натуральных чисел называется
подстановкой 
-й степени.
Подстановка обычно записывается в виде таблицы из двух строк, где верхняя строчка – исходное множество, а нижняя – его отображение. Верхняя и нижняя строки при этом являются перестановками.
ПРИМЕР:
Запись подстановки, в которой в верхней строчке числа записаны строго по возрастанию, называется канонической.
! Перестановка столбцов в таблице никак не меняет само отображение. Например,
1 |
2 |
3 |
4 |
и |
2 |
1 |
4 |
3 |
|
2 |
3 |
1 |
4 |
3 |
2 |
4 |
1 |
||
|
— одна и та же подстановка E4 (двойке в верхней строке всё равно соответствует тройка в нижней и т.д). Любая перестановка приводится к каноническому виду изменением порядка столбцов – последовательным выполнением нескольких транспозиций в верхней строке и соответствующих им транспозиций в нижней строке. Т.к. одновременно меняем чётность в обеих строках, соотношение этих чётностей сохраняется.
Произведение или композиция перестановок по сути, можно понимать как действие
одной перестановки на другую.
ПРИМЕР 1. Найти произведение подстановок можно так (простой прямой способ)
Первой действует подстановка слева. Первая подстановка переводит один в два, а вторая два в семь, значит произведение переводит один в семь и т.д.
ПРИМЕР 2: Также по определению произведение σ • τ можно вычислять так: в подстановке σ переставляем столбцы так, что первая строчка в σ совпадает с последней строчкой в τ. Тогда произведением будет подстановка, у которой первая строчка — стандартная, а вторая строчка — это вторая строчка из σ.
Произведение двух подстановок есть снова подстановка . |
|
|
||
! Произведение подстановок ассоциативно: τ |
(σ α) = ( τ |
|
σ ) α |
|
!! |
|
: |
|
|
|
Произведение подстановок некоммутативно τσ ≠ στ. |
|||
Тождественная (или единичная) подстановка - отображающая каждый элемент в
себя: |
. |
|
|
. Например: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|||
И для |
тождественной подстановки умножение коммутативно и равно |
|
|
|
|
|||||||
|
|
σ е |
= е σ = σ |
, для любой σ Sn, где Sn - группа всех возможных |
||||||||
перестановок длины n (симметрическая группа) |
|
|
|
|
|
|||||||
|
Тождественная подстановка играет роль единицы в симметрической группе Sn |
|
||||||||||
Обратная подстановка σ-1 |
по отношению к подстановке σ – подстановка, умножение |
|||||||||||
|
|
|
|
|
|
|
|
|
σ |
|
|
|
которой слева или справа на исходную даёт тождественную подстановку. |
||||||||||||
σ σ-1= σ-1 |
|
σ = е |
|
|
|
|
|
|
|
|||
Обратная подстановка существует и является единственной для каждой |
|
|
Sn. |
|||||||||
|
|
Таблицу обратной подстановки можно получить, если просто |
поменять местами |
|||||||||
|
|
|
|
|
|
|
||||||
верхнюю и нижнюю строки таблицы исходной подстановки. Например:
, 
.
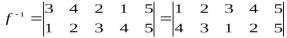Также подстановки можно представлять:
Пример Задана подстановка |
|
. |
|
|
|
1) в графической форме, проводя стрелки от каждого |
|
||||
элемента к элементу |
(см. рисунок) |
|
|||
2) |
строкой: F = [23145] – в строке на i-м месте стоит элемент F |
(i); |
|||
3) |
в виде произведения циклов: |
F = (123)(45) – каждая |
|
||
скобка является отдельным циклом, в каждой скобке следующий |
|
||||
элемент получен из предыдущего, |
а первый элемент получен из последнего |
применением |
|||
транспозиции.
Разложение подстановки в произведение независимых циклов устроено просто:
достаточно уметь представлять цикл произвольной длины в виде произведения транспозиций.
Закономерность достаточно простая: (abc)=(ab)(ac); (abcd)=(ab)(ac)(ad); (abcde)=(ab)(ac)(ad)(ae), и
так далее. Каждое из равенств легко проверяется непосредственно.
14.Что такое перестановка?
Перестановка – упорядоченный набор (=множество) n элементов множества E,
то есть расположение их в определённом порядке.
Если множество Е состоит из n-элементов, то число перестановок (то есть вариантов расположения n элементов) равно n!, где n — длина перестановки.
Перестановки бывают четными и нечетными.
15.Что такое транспозиция перестановки?
Транспозиция - перемена местами двух элементов перестановки.
Теор.1 Все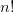 
-перестановок длины 
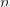можно расположить одну за другой таким образом,
что каждая последующая получается из предыдущей одной транспозицией. Причем можно начинать такое упорядочивание с любой перестановки.
Следствие. Число четных перестановок из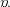 
символов равно числу нечетных, т.е. 
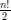(при любом 
).
Теор.2 Любая транспозиция меняет чётность перестановки на противоположную.
16.В каком случае два числа образуют инверсию в перестановке?
Инверсию (нарушение порядка) образует пара элементов в перестановке когда
меньшее из них расположено правее большего.
Каждой перестановке можно сопоставить число инверсий в ней, которое подсчитывается так: для каждого из элементов определяют количество стоящих правее его меньших чисел, и полученные результаты складываются.
Перестановка называется четной, если число инверсий в ней четно, и нечетной –
если инверсий в ней нечётное количество.
ПРИМЕР: Найти число инверсий в перестановке: (5,3,1,4,2,6).
Рассмотрим элементы слева направо по очереди, считая инверсии для каждого.
1) |
инверсии с 1-м элементом (5,3) (5,1) (5,4) и (5,2) => 4 |
инверсии |
2) |
инверсии с 2-м элементом (3, 1) и (3,2) => 2 инверсии |
|
3) |
инверсии с 3-м элементом 1 => 0 инверсий, т.к. 4,2 и |
6 больше 1 |
4)инверсии с 4-м элементом (4,2) => 1 инверсия
5)инверсии с 5-м элементом 2 => 0 инверсий, т.к. 6 больше 2.
Итого в перестановке 4 + 2 + 0 + 1 + 0 = 7 инверсий. Перестановка нечетная.
17.Какая перестановка называется четной?
Четная перестановка - содержащая четное количество инверсий.
*Число инверсий в перестановке подсчитывается так: для каждого из элементов определяют количество инверсий (стоящих правее его меньших чисел), и полученные результаты складывают.
18.Какая перестановка называется нечетной?
Нечетная перестановка - содержащая нечетное количество инверсий.
*Число инверсий в перестановке подсчитывается так: для каждого из элементов
определяют количество инверсий (стоящих правее его меньших чисел), и полученные результаты складывают
19.Как влияет транспозиция на четность перестановки?
Любая транспозиция (то есть перемена местами двух любых элементов) меняет
чётность перестановки на противоположную.