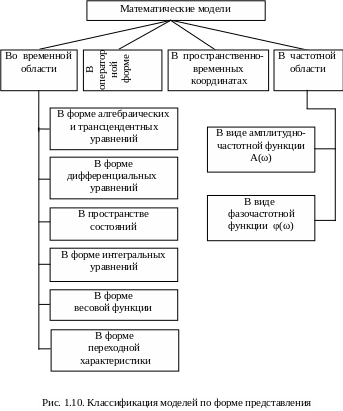
1.3.4. Классификация математических моделей
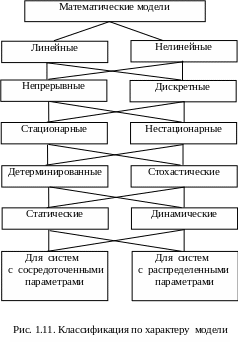
Математические модели можно классифицировать по форме их представления (рис. 1.10). За основу второй классификации (рис. 1.11) взят характер модели.
2. Математические модели в форме
СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
2.1. Области применения
Исследование некоторых физических систем приводит к математическим моделям в форме систем линейных алгебраических уравнений (СЛАУ). Иногда СЛАУ появляются в процессе математического моделирования как промежуточный шаг (этап) в решении более сложной задачи. Есть значительное число научно-технических задач, в которых математические модели сложных нелинейных систем посредством дискретизации или линеаризации сводятся к решению СЛАУ.
Примеры задач, использующих математические модели в форме СЛАУ:
1) при проектировании и эксплуатации электротехнических устройств требуется проведение расчета и анализа их работы в стационарных режимах. Задача сводится к расчету эквивалентных схем, в основе которого лежит формирование и решение СЛАУ;
2) при
построении математической модели,
связывающей функциональной зависимостью
некоторые параметры x,
y
исследуемого объекта на основании
полученных в результате эксперимента
данных
,
где i
= 1,2,3, .... ,n
(задачи аппроксимации данных);
3) при исследовании процессов в системах, математические модели которых строятся в классе дифференциальных уравнений в частных производных. В результате разностной аппроксимации исходной модели при определенных условиях приходят к математическим соотношениям в форме СЛАУ;
4) сущность многих физических процессов математически отображается с помощью интегральных уравнений. Ввиду сложности решения многих из них исследователь предпочитает свести задачу к решению модели в форме СЛАУ, используя известные методы аппроксимации.
5) исследование систем автоматического регулирования в установившемся режиме приводит во многих случаях к статическим моделям в форме СЛАУ.
Система линейных уравнений порядка n имеет вид:
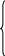
(2.1)
или в векторно-матричной форме:
(2.2)
где
– вектор свободных членов;
– вектор неизвестных;
A
– матрица коэффициентов системы,
размером
.
2.2. Методы решения
Методы решения СЛАУ делятся на две группы: прямые (точные) и итерационные (приближенные).
Прямые методы позволяют получить решение за конечное число шагов. Итерационные методы построены по принципу многократного вычисления последовательных приближений, сходящихся к искомому решению.
Прямые методы целесообразно использовать для решения систем сравнительно небольшой размерности с плотно заполненной матрицей (матрицей, имеющей малое количество нулевых элементов). Итерационные методы предпочтительнее в задачах большой размерности со слабо заполненными матрицами.
К прямым методам относятся метод определителей, метод Гаусса и его модификации, метод LU-разложения, матричный метод и др. К разряду итерационных методов принадлежат метод простой итерации, метод Зейделя.