8.2. Линейные непрерывные детерминированные системы

Уравнение состояния линейной непрерывной детерминированной системы при имеет вид:

(8.6)

где F(t) – матрица коэффициентов размерности n n;

G(t) – вектор коэффициентов (n-мерный);

u(t) – входное воздействие.

Д инамическая модель (8.6) может быть отображена с помощью структурной схемы (рис. 8.2). Двойные стрелки на рис. 8.2 отображают векторный характер сигналов.

Вектор состояния X(t) определяется путем решения уравнения состояния (8.6):

(8.7)

где Ф(t,t₀) – переходная матрица состояний размерности , которая определяется путем решения дифференциального уравнения

(8.8)

при начальных условиях:

Ф(t₀, t₀) = I, (8.9)

где I – единичная матрица, и замене t₀ на τ.

Стационарная физическая система. Уравнение состояния стационарной системы имеет вид:

(8.10)

где F и G не зависят от времени.

Решение уравнения (8.10) значительно упрощается.

Переходная матрица состояний определяется так:

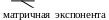(8.11)

где

− (8.12)

экспоненциальный ряд.

Тогда

(8.13)

(8.14)

Решение динамической модели (8.10) запишется в виде:

(8.15)

При определении матричной экспоненты можно ограничиться первыми четырьмя членами ряда (8.12), что обеспечит достаточную точность результата при малых значениях .

8.3. Формирование математической модели в пространстве состояний по дифференциальному уравнению n-го порядка

Вариант 1. Пусть физическая система описывается таким дифференциальным уравнением:

. (8.16)

Введем оператор Вынесем функции y и u за скобки. Тогда уравнение (8.16) примет вид:

(8.17)

Введем обозначения:

(8.18)

(8.19)

Получим:

A(p)y =B(p)u. (8.20)

Умножим обе части уравнения (8.20) на , после чего введем обозначение x₁:

(8.21)

Тогда

(8.22)

Введем еще обозначения:

(8.23)

Сделаем подстановку обозначений (8.23) в выражение (8.22):

(8.24)

или

(8.25)

откуда выразим

(8.26)

Объединяя уравнения (8.26) и (8.23), получим систему уравнений в нормальной форме или в форме Коши, т. е. уравнения состояния:

(8.27)

или уравнение состояния в векторно-матричной форме при X(t₀) = X₀:

(8.28)

где

Вариант 2. Пусть физическая система описывается дифференциальным уравнением:

(8.29)

Введем обозначение:

y(t) = x₁(t) = x₁, (8.30)

сделаем подстановку обозначения (8.30) в уравнение (8.29):

(8.31)

Члены уравнения (8.31), не содержащие производных, сгруппируем в правой части уравнения:

(8.32)

Введем обозначение:

(8.33)

сделаем подстановку обозначения (8.33) в уравнение (8.32) и проинтегрируем полученное выражение:

. (8.34)

Сгруппируем в правой части уравнения (8.34) члены, не содержащие производных:

. (8.35)

Введем обозначение:

(8.36)

Сделаем подстановку обозначения (8.36) в уравнение (8.35) и проинтегрируем полученное выражение:

(8.37)

Из уравнения (8.37) выразим :

(8.38)

Объединив уравнения (8.33), (8.36) и (8.38), получим систему уравнений состояния в форме Коши:

(8.39)

или в векторно-матричной форме при X(t₀) = X₀:

(8.40)

где