8. Математические модели в пространстве состояний

8.1. Основные понятия

Динамическая система – это физическая система, состояние которой изменяется во времени под действием входных сигналов и (или) возмущений.

Состояние динамической системы полностью и однозначно определяется совокупностью переменных состояния x1, x2, x3, ... , xn.

Состояние системы в момент времени t₁ может быть определено, если известны состояние ее в момент времени и значение входного воздействия в момент времени t₁.

Пространство состояний – это пространство, в котором каждой точке соответствует определенное состояние системы, а положение этой точки определяется значениями переменных состояния.

Вектор состояния – это совокупность переменных состояния:

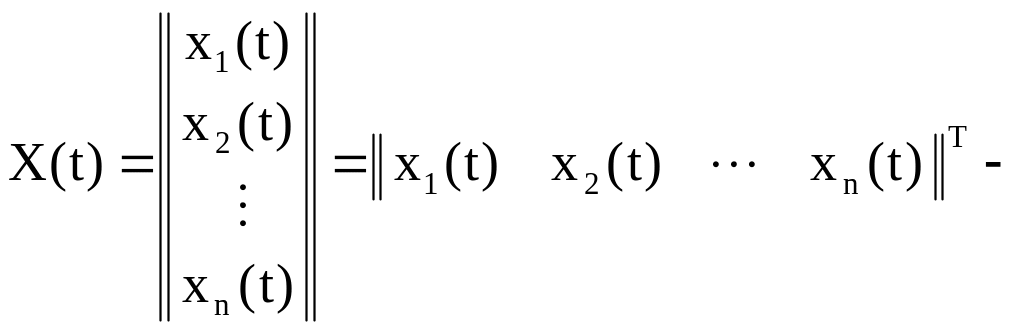^(8.1)

n-мерный вектор.

Начальное состояние системы характеризуется начальным вектором состояния:

(8.2)

Трехмерное пространство состояний. Вектор состояния

. (8.3)

Координатами вектора состояния X(t) являются три переменных состояния: x₁, x₂, x₃.

К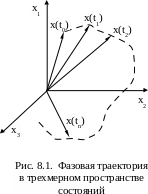 онец вектора состояния X(t) при изменении времени t описывает кривую, которая называется фазовой траекторией (рис. 8.1). Таким образом, фазовая траектория отображает процесс изменения состояния системы во времени.

Вектор состояния X(t) будет полностью и однозначно определять состояние физической системы только в том случае, если его размерность будет равна размерности системы.

Выбор переменных состояния для физической системы неоднозначен, т. е. для одной системы возможны различные комбинации переменных состояния.

Уравнение состояния системы– динамическая модель (модель динамики системы) – описывает поведение динамической системы, оно представляет собой систему обыкновенных дифференциальных уравнений первого порядка в нормальной форме или в форме Коши.

Уравнение состояния системы в векторно-матричной форме имеет вид:

(8.4)

где X – n-мерный вектор состояния;

t – независимая переменная;

u – вектор входных воздействий (в общем случае),

. (8.5)

Уравнение (8.4) описывает динамическую систему. Решение уравнения (8.4) представляет собой математическую модель про-цесса X(t), имеющего место в данной системе при заданных начальных условиях и входном воздействии u(t). Таким образом, в системе может рассматриваться множество процессов, соответствующих заданному множеству начальных условий и множеству входных воздействий.

Достоинства математического описания физических систем в прост-ранстве состояний:

возможность с единой позиции рассматривать стационарные и нестационарные, линейные и нелинейные системы;

возможность учитывать ненулевые начальные условия;

наличие достаточного количества численных методов реализации таких математических моделей;

возможность более разностороннего изучения физической системы путем формирования нескольких моделей в разных пространствах состояний.