Вопрос 4
Закон
сохранения энергии и импульса
Рассмотрим
механическую систему, состоящую из n
тел, с массами m1, m2, ... , mn и скоростями
v1, v2, ... , vn. Пусть F1', F2', ... , Fn' - равнодействующие
внутренних сил, действующих на каждое
из n тел, a F1', F2', ... , Fn' - равнодействующие
внешних сил. Применим второй закон
Ньютона для каждого из n тел рассматриваемой
механической системы:
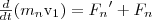
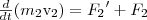
Складывая
почленно эти уравнения, получаем
d/dt(m1v1+m2v2+..+mnvn)=F’₁+F’₂+..+F’n+F₁+F₂+..+Fn
Но
так как векторная сумма внутренних сил
механической системы равна нулю по
третьему закону Ньютона, то
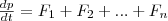 ,
где
,
где
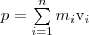 -
импульс механической системы. Значит,
производная по времени от импульса
механической системы равна векторной
сумме внешних сил, действующих на
систему. В случае замкнутой системы:
-
импульс механической системы. Значит,
производная по времени от импульса
механической системы равна векторной
сумме внешних сил, действующих на
систему. В случае замкнутой системы:
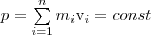 есть
закон сохранения имаульса: импульс
замкнутой системы сохраняется, т. е. не
изменяется с течением времени.
есть
закон сохранения имаульса: импульс
замкнутой системы сохраняется, т. е. не
изменяется с течением времени.
T+П=E=const
-закон сох.энергии:в системе сил между
которыми действует только консервативные
силы,полная мех-ая энерг.сохр,т.е. не
измен.со времн

