Лекция № 16. Гироскопические измерители истинного курса (гирокомпасы)

В качестве измерителей курса могут использоваться трехстепенные и двухстепенные гирокомпасы. Двухстепенные могут использоваться только на неподвижном основании (артиллерийский, маркшейдерский).

Гирокомпасы на базе трехстепенного гироскопа.

Могут быть двух типов:

1. Гиромаятниковый гирокомпас

2. Акселерометрический гирокомпас;

Гирокомпас должен в любой момент определять направление на север. Принцип действия компаса на базе трехстепенного гироскопа основан на использовании горизонтальной составляющей вращения Земли, которая все время ориентирована на Север, а так же на использовании смещения центра масс гироузла гироскопа (гиромаятниковый ГК) относительно оси г ироузла вниз.

Изобразим кинематическую схему обобщенного гирокомпаса (см. рис.1 при угле ). На рис.2 изображен гирокомпас в двух проекциях со стороны оси OZ.

Если рассматриваем гиромаятниковый гирокомпас, то акселерометр А и и на схеме будут отсутствовать.

Если рассматриваем акселерометрический ГК, то акселерометр А и и есть на схеме, однако нет маятниковости гирокомпаса за счет смещения центра масс вдоль отрицательного направления оси OY , то есть Р=0 и l=0, где Р – вес груза, l – расстояние от центра масс груза до начала координат.

Гирокомпас представляет собой трехстепенной гироскоп, ось наружной рамки которого должна быть вертикальна, ось подвеса НР - OY₁, ось подвеса гироузла - OZ₁, вдоль отрицательной оси OY имеется положительное смещение центра масс. На схеме не показано устройство съема сигнала, которое должно быть на оси наружной рамки.

На практике трехстепенной гироскоп выполняется в виде сферы, которая плавает и центрируется в жидкости (это делается для уменьшения моментов трения).

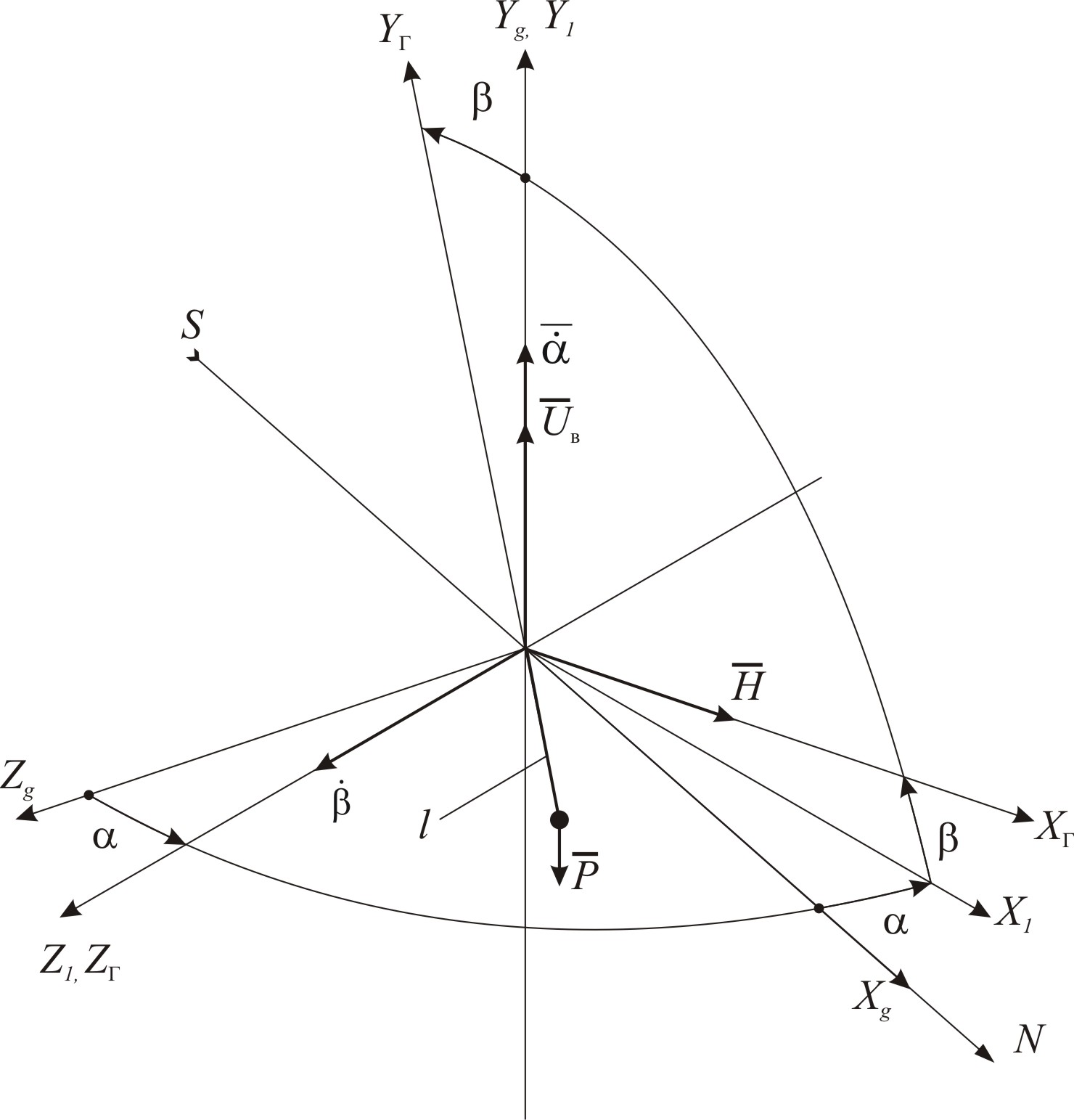
Системы координат и прецессионные уравнения

OX_gY_gZ_g – «земная» система координат. Ось OX_g направлена по полуденной линии, OY_g – по местной вертикали места.

OX₁Y₁Z₁ – система координат, связанная с наружной рамкой. Ось OY₁ – ось подвеса наружной рамки. Вокруг нее гирокомпас поворачивается с угловой скоростью на угол .

А_ - матрица элементарного поворота на угол  (матрица направляющих косинусов).

Рис.3. Системы координат

Матрицы элементарных поворотов составляют следующим образом: вверху пишется исходная система координат, слева (справа) – полученная. В соответствующих ячейках матрицы пишутся коэффициенты, с которыми единичные векторы исходной системы координат проектируются на оси координат конечной системы.

Запишем выражение для матрицы элементарных поворотов А_:

.

Свойство матриц элементарных поворотов – их определитель равен единице. Это говорит от том, что преобразуемые системы ортогональны.

- система координат, связанная с гироузлом (с внутренней рамкой гирокомпаса). Ось (или OZ₁)– ось подвеса внутренней рамки. Вокруг нее гироузел поворачивается с угловой скоростью на угол .

;

Определим матрицу элементарных поворотов системы координат OXYZ на угол :

Определение матрицы направляющих косинусов А между осями OX_gY_gZ_g и :

САМОСТОЯТЕЛЬНО! Получить матрицу А перехода от OX_gY_gZ_g к двумя способами:

1. перемножением матриц А_ и А_. . Матрица

2. геометрическим проектированием ортов системы координат OX_gY_gZ_g на оси системы координат .

Полученные двумя методами матрицы должны совпасть.

Матрицы направляющих косинусов вводились для того, чтобы в дальнейшем посчитать момент от силы веса Р.

Прецессионные уравнения гиромаятникового гирокомпаса

Составляем прецессионные уравнения движения гирокомпаса методом Даламбера:

М_Г - гироскопический момент;

М_Р - момент от груза весом Р.

М_др - вредный момент дрейфа.

Сделаем некоторые допущения:

1) Основание гирокомпаса неподвижно или движется с постоянной скоростью.

2) Углы  и  - малы, так как необходимо построить прецизионный прибор, определяющий меридиан с высокой точностью (порядка ).

Прецессионные уравнения записываем относительно осей подвеса наружной и внутренней рамки.

Уравнение относительно оси подвеса наружной рамки – оси OY₁.

Гироскопический момент относительно этой оси равен:

Сила Р направлена параллельно оси подвеса НР и не создает момента. Тогда запишем прецессионное уравнение движения гирокомпаса относительно оси подвеса НР:

(1)

Уравнение относительно оси подвеса внутренней рамки – оси OY₁.

Гироскопический момент относительно этой оси равен:

Момент от силы Р отрицателен и из геометрических соображений равен

.

Тогда прецессионное уравнение движения гирокомпаса относительно оси внутренней рамки примет вид:

(2)

Вычисление момента от веса груза на основании общего подхода то есть .

Или в развернутой форме

(3)

– орты осей системы координат .

- проекции вектора на оси системы координат . Они определяются по следующей формуле:

(4)

А – матрица элементарных поворотов определена в приложении к лекции №16.

Подставив (4) в (3), определим момент груза относительно осей гироузла

.

То есть в линейной постановке момент груза действует только относительно оси подвеса гироузла и равен

что совпадает со значением полученным геометрически.

Записываем прецессионные уравнения движения (1) и (2) с учетом допущения о малости углов.

;

.

Величина называется направляющим моментом гирокомпаса. При направляющий момент стремится к нулю и ГК становиться неработоспособным. Так как направляющий момент должен преодолевать дрейф. То чем меньше вредные моменты, то тем на больших широтах можно использовать гирокомпас (обычно на широтах до 80⁰).

Поделим обе части этих уравнений на Н

; (5)

. (6)

В полученных уравнениях

- максимальная угловая скорость прецессии от грузиковой коррекции;

- угловая скорость дрейфа относительно оси OY₁;

- угловая скорость дрейфа относительно оси .

Таким образом, получили систему дифференциальных уравнений движения гирокомпаса, которые могут быть решены при наличии начальных условий.