Определенный интеграл.
Связь определенного и неопределенного интегралов задается формулой Ньютона – Лейбница:
т. е. определенный интеграл от непрерывной функции f (x) равен приращению первообразной функции F(x) на отрезке [a, b].
Формула Ньютона – Лейбница позволяет вычислять определенный интеграл, используя методы вычисления неопределенного интеграла, рассмотренные в предыдущей главе.
Пример 8.8.
Вычислить интеграл
Решение. Используя свойства определенного интеграла и формулу Ньютона – Лейбница, получим:
Пример 8.9.
Вычислить интеграл
Решение. Полагая
имеем
Найдем
новые пределы интегрирования:
Имеем:
Пример 8.10.
Вычислить интеграл
Решение. Применяя формулу интегрирования по частям, для определенного интеграла
найдем:
=
=
=
Геометрические приложения определенного интеграла
Вычисление площади в декартовых координатах
Если функция
непрерывна
на [a,
b]
и положительна, то площадь криволинейной
трапеции, ограниченной функцией
,
двумя прямыми
и
и отрезком [a,
b]
оси абсцисс, вычисляется по формуле
если
на отрезке [a,
b],
то,
Площадь фигуры,
ограниченной двумя непрерывными
функциями
и
и двумя прямыми
и
,
где
на отрезке [a,
b],
находится по формуле:
Вычисление площадей с помощью определенного интеграла осуществляется в следующим порядке:
1) делается рисунок фигуры, площадь которой необходимо найти;
2) находятся пределы интегрирования;
3) подбирается нужная формула;
4) вычисляется значение площади.
Пример 8.11.
Вычислить площадь фигуры, ограниченной
параболой
прямыми
и осью абсцисс.
Решение.
Построим криволинейную трапецию
Пределы интегрирования:
Площадь вычисляем
по формуле
Получаем
(кв.
ед.).
Пример 8.12.
Вычислить
площадь фигуры, ограниченной параболой
осями координат и прямой
Решение. На рисунке 2. изображена фигура, площадь которой надо найти.
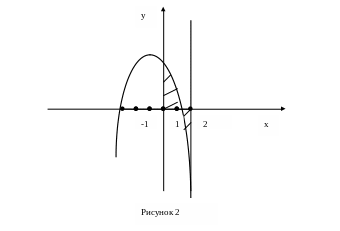
Функция
на отрезке [0, 2] меняет знак. Следовательно,
промежуток интегрирования [0, 2] необходимо
разбить на два промежутка:
и
.
Получим:
(кв.
ед).
Пример 8.13.
Вычислить площадь фигуры, ограниченной
параболой
и
прямой
Решение. Сделаем рисунок плоской фигуры, заключенной между параболой и прямой (рисунок 3).
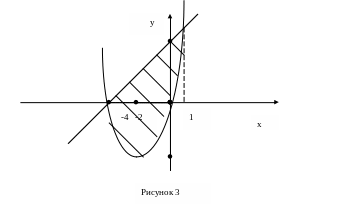
Найдем пределы
интегрирования, для этого решим систему
уравнений
и получим
Следовательно,
пределы интегрирования:
Вычислим площадь:
(кв. ед.).
Вычисление объема тел вращения
Объем
тела, образованного вращением вокруг
оси Ох
криволинейной трапеции, ограниченной
непрерывной кривой
осью
абсцисс и двумя прямыми
и
находится
по формуле
Объем
тела, образованного вращением вокруг
оси Оу
криволинейной трапеции, ограниченной
непрерывной кривой
осью ординат и двумя прямыми
и
находится по формуле
Пример
8.14
Вычислить объем тела, ограниченного
поверхностью вращения параболы
вокруг оси Ох
и плоскостью
Решение. Найдем Vx согласно приведенной выше формуле:
(куб. ед.).
Пример
8.15.
Найти объем тела, образованного вращением
вокруг оси Оу
фигуры, ограниченной кривой
и отрезком
оси ординат.
Решение.
Записав уравнение данной кривой в виде
и
используя формулу вычисления объема,
получим
(куб. ед.).
Вычисление длины дуги кривой в прямоугольных координатах
Если производная
функции
является
непрерывной функцией на отрезке [a,
b],
то длина дуги кривой
,
заключенная между точками с абсциссами
и
,
находится по формуле
Пример
8.16.
Найти длину дуги цепной линии
между прямыми
и
Решение.
Найдем производную функции
:
и вычислим длину дуги кривой:
Вычисление площади поверхности тела вращения
Если производная функции является непрерывной функцией, то кривая называется гладкой кривой. Площадь поверхности, образованной вращением вокруг оси Ох дуги гладкой кривой между точками с абсциссами и , вычисляется по формуле
Пример 17.
Найти площадь поверхности вращения
вокруг оси Ох
дуги кубической параболы
при
Решение. Используем приведенную выше формулу для вычисления площади:
Вычислим этот
интеграл методом подстановки. Обозначим
тогда
Пересчитаем
пределы интегрирования: при
при
Получаем
(кв.ед.).