Цель работы: целью работы является изучение распределения потоков мощности в простых замкнутых сетях, а также определение напряжений в узлах замкнутых электрических сетей

1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

В простых сетях есть узлы, питающихся по двум ветвям, но нет узлов, получающих питание более чем по двум ветвям, отсутствуют узлы, с которыми соединены три и более ветвей. Характерным частным видом простой замкнутой сети является кольцевая сеть (рисунок 1).

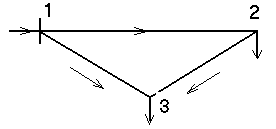
Рисунок 1 – Схема простой замкнутой сети

Она содержит один замкнутый контур. В качестве источников питания могут служить или электрические станции, или шины подстанции, в свою очередь связанные сетью с электростанции.

Кольцевая сеть может быть представлена в виде линии с двухсторонним питанием. Действительно, если источник питания в узле 1 мысленно разделить на два и представить в виде узлов 1 и 4, то из кольцевой сети получим линию с двухсторонним питанием (рисунок 2)

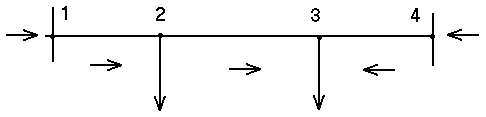
Рисунок 2 – Схема сети с двухсторонним питанием

К достоинствам замкнутых сетей следует отнести повышенную надежность электроснабжения потребителей, меньше потери мощности, к недостаткам – сложность эксплуатации, удорожание за счет дополнительных линий. Расчет замкнутых сетей сложнее, чем разомкнутых.

Электрическая схема простой замкнутой сети представлена на рисунке 3.

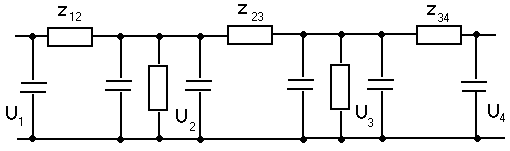
Рисунок 3 – Электрическая схема замкнутой сети

Схема замещения простой сети представлена на рисунке 4.

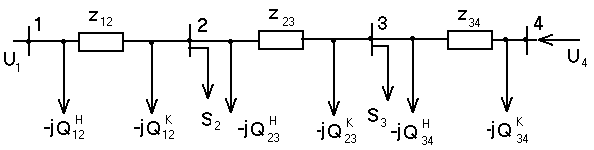
Рисунок 4 – Схема замещения

1. Расчет без учета потерь мощности

Заданы одинаковые напряжения по концам линии U₁ = U₄.

Определим приближенное потокораспределение в кольце с целью выявления точки потокораздела. Принимаем следующие допущения:

а) пренебрегаем потерями;

б) предполагаем, что ток участка определяется по номинальному напряжению

.

При равенстве напряжении источников питания на основании второго закона Кирхгофа можно записать

.

Если заменим в последнем выражении все комплексные величены на сопряженные, то получим следующее уравнение

. (1)

Так как потери мощности не учитывается, первый закон Кирхгофа для узлов 2 и 3 можно записать так:

S₂₃ = S₁₂ – S_2, (2)

S₄₃ = S₃ – S₂₃ = – S₁₂ + S₂ + S₃ . (3)

Подставив значения мощности (2) и (3) в (1), получим уравнение с одним неизвестным:

. (4)

Отсюда находим значение потока мощности S₁₂.

. (5)

Аналогично для потока мощности S₄₃:

. (6)

Проверяют правильность определения потоков мощности на головных линиях кольца по условию:

S₁₂ + S₄ = S₂ + S₃. (7)

Находят поток в линию 23 по первому закону Кирхгофа для узла 2

S₂₃ = S₁₂ – S₂. (8)

Узел (2)3 – точка потокораздела. Мощность, поступающая с электростанции и определения без учета потерь мощности.

S₁=S₁₂ + S₄₃. (9)

2. Расчет с учетом потерь мощности

Предположим, что направления мощностей соответствуют точка потокораздела в узле 3, который отмечен залитым треугольником. «Разрежем» линию в узле 3 (рисунок 5) и рассчитываем потоки мощности в линиях 13 и 43.

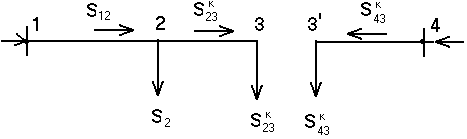
Рисунок 5 – Схема разрезанной линии

Необходимо вычесть из потоков мощности S₁₂, S₂₃ ,S₃₄ мощности, генерируемые емкостными составляющими сопротивлений линии:

S₁₂^к=S₁₂ – jQ_с12, (10)

S₂₃^к=S₂₃ – jQ_с23, (11)

S₃₄^к=S₃₄ –jQ_с34. (12)

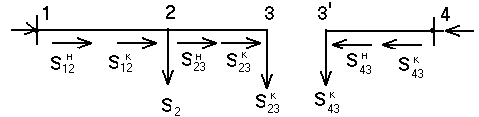
Рисунок 6 – Схема с точкой потокораздела

Потери мощности в линии 23

, (13)

Мощность в конце линии 12

S₁₂^к = S₂₃^к + S₂₃+ S₂. (14)

Мощность в начале линии 12

S₁₂^н = S₁₂^к + S₁₂. (15)

Потери мощности в линии 12:

, (16)

Рассчитываем потоки мощности линии 43. Мощность в конце линии S₄₃^к найдена ранее.

Потери мощности в линии 43

. (17)

Мощность в начале линии:

S₄₃^н = S₄₃^к + S₄₃. (18)

Мощность, потребляемая с шин электростанции

S₁ = S₁₂^н + S₄₃^н. (19)

3. Определение напряжений в узлах

Падение напряжения U₄₃

, (20)

U₃^’=U₁ – U₄₃. (21)

Падения напряжения U₁₂

, (22)

U₂=U₁ – U₁₂. (23)

Падения напряжения U₂₃

, (24)

U₃ = U₂ – U₂₃. (25)

Наибольшая потеря напряжения в номинальном режиме, определяется без учета потерь мощности

U_нб = U₁₃ = U₁₂ + U₂₃. (26)