2.18. Теорема существования первообразной непрерывной функции

В предыдущем пункте фактически была доказана теорема, решающая поставленную в главе 1 (п.1.3) проблему существования первообразной. Сформулируем эту теорему.

Теорема 2.5. Если функция непрерывна на отрезке , то для этой функции существует первообразная на отрезке .

Действительно, в силу (2. 17) первообразной для функции на отрезке является определённый интеграл с переменным верхним пределом, а именно функция

,

Напомним, что неопределённый интеграл от функции представляет собой семейство первообразных этой функции. Итак, имеем соотношение

(2.19)

связывающее неопределённый интеграл с определённым интегралом.

2.19. Интеграл с переменным верхним пределом и неэлементарные функции

Обычно при построении новых функций из известных используются арифметические операции и операция составления сложной функции – операция суперпозиции. Например, функция получена в результате умножения линейной функции и сложной функции , составленной из степенной и показательной функций.

Арифметические действия и операция суперпозиции, применённые конечное число раз к элементарным функциям, вновь приводят к элементарным функциям.

Интеграл с переменным верхним пределом есть функция, построенная принципиально другим способом. Здесь элементарность функции , вообще говоря, не обеспечивает элементарности функции Например, функции , , не являются элементарными, т.к. они являются первообразными для функций , , которые не имеют первообразных в классе элементарных функций. Напомним, что интегралы от таких функций называют «неберущимися» (п.1. 11).

Геометрический смысл интеграла с переменным верхним пределом позволяет по-новому взглянуть на некоторые известные функции. Например,

(2.20)

(будет показано в п.2.19). Поэтому значение функции в точке численно равно площади под гиперболой на отрезке (рис.2. 18).

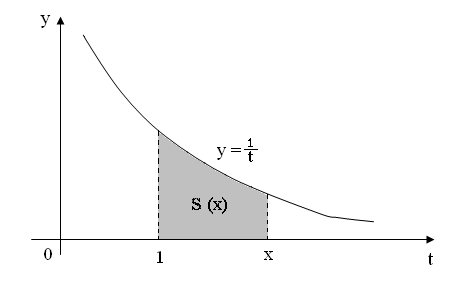
Рис.2.18

2.20. Формула Ньютона-Лейбница

Теорема 2.6. (Основная теорема интегрального исчисления). Пусть функция непрерывна на отрезке и – любая первообразная для на . Тогда определённый интеграл от функции по равен приращению первообразной на этом отрезке, т.е.

(2.21)

Доказательство. Пусть – некоторая первообразная для . По теореме 2.4 функция также является первообразной для функции . Следовательно, функции и являются первообразными одной и той же функции на отрезке . Поэтому существует число С, такое, (следствие 1.2).

Тогда для приращения первообразной на имеем равенство

Поскольку определённый интеграл по вырожденному промежутку равен нулю, т.е. получаем формулу (2.21).

Формулу (2.21) называют формулой Ньютона-Лейбница.

Замечание 2.5. Напомним, что разность не зависит от того, о какой именно первообразной функции на промежутке идёт речь (следствие 1.2). Поэтому в формуле (2.21) в качестве функции может быть использована любая первообразная функции из семейства

Отметим, что ценность формулы Ньютона-Лейбница¹⁾ состоит в том, что она устанавливает равносильность двух важных задач для функции, непрерывной на замкнутом промежутке: задачи нахождения первообразной и задачи вычисления предела интегральных сумм. Сама по себе эта формула не решает ни одной из этих задач.

_________________________________________

¹⁾ Формулы Тейлора и Ньютона-Лейбница – две великие формулы математического анализа (В.П. Хавин.)

Вычисление определённого интеграла с использованием формулы Ньютона-Лейбница осуществляется в два шага: на первом шаге, используя методы нахождения неопределённого интеграла, находят первообразную для подынтегральной функции ; на втором шаге применяется формула Ньютона- Лейбница – находится приращение первообразной на промежутке интегрирования , равное искомому интегралу.

Введём обозначение для приращения первообразной которое удобно использовать при записи решений. По определению положим

(2.22)

Примеры 2.7. Вычислить интегралы 1) ; 2) ;

Решение. 1). Произвольная первообразная для функции имеет вид Возьмём первообразную, у которой Тогда