2.13. Знак интеграла
Если всюду на отрезке функция сохраняет знак, то интеграл есть число того же знака, что и функция .
Пусть для
определённости
на
.
Тогда любая интегральная сумма
функции
на отрезке
неотрицательна, поскольку
.
Переходя к пределу при
(
-– ранг дробления) в неравенстве
,
получим
.
Итак,
Например,
.
2.14. Интегрирование неравенства
Если для непрерывных
на отрезке
функций
и
всюду на
имеет место соотношение
,
то обе части этого неравенства можно
интегрировать почленно, т.е.. выполнено
соотношение
,
Пусть
- дробление отрезка
,
оснащение
дробления
.
Из неравенства
следует
аналогичное неравенство для интегральных
сумм:
.
Переходя в этом
неравенстве к пределу при
,
получим соответствующее неравенство
для интегралов.
Итак,
Доказанное утверждение имеет простой геометрический смысл для функций, принимающих на отрезке только неотрицательные значения. Площадь фигуры, ограниченной сверху графиком функции не превосходит площади фигуры, ограниченной сверху графиком функции (рис.2.12).
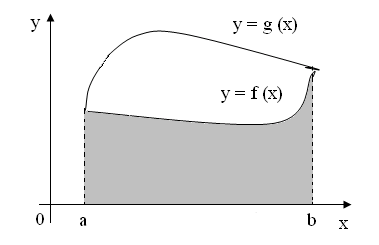
Рис. 2.12
Оценки интегралов
Пусть функция
непрерывна на отрезке
(
),
и всюду на
этом отрезке имеет место неравенство
где
и
–
некоторые числа. Тогда
|
(2.11).
В силу п. 2.13 имеем
Используя далее свойство интеграла от постоянной функции (формулу (2.9)) нетрудно убедиться в справедливости соотношения (2.11).
Соотношение (2.11) имеет простой геометрический смысл ( рис.2.13):
значение
определённого интеграла от неотрицательной
на отрезке
функции
,
т. е. величина площади фигуры ограниченной
сверху графиком этой функции оценивается
:
сверху – величиной площади прямоугольника с основанием и
высотой ;
снизу – величиной площади прямоугольника с основанием и
высотой
Рис.2.13
Из рисунка (2.13) видно, что оценка (2.11) может оказаться очень грубой. Она удовлетворительна только тогда, когда на большей части отрезка функция близка к или к .
Пример 2.4.
Оценим интеграл
от степенной функции.
Решение. Далее (п. 2.12) будет доказано, что
(2.12)
Интеграл вычисляет площадь криволинейного треугольника, ограниченного сверху графиком функции , вписанного в квадрат со стороной , равной единице (рис. 2.14).
Рис. 2.14.
В этом случае
и оценка (2.11) принимает вид
(2.13)
Если
– малое положительное число, то
криволинейный треугольник «почти
заполняет» квадрат и
,
т.е. верхняя оценка данного интеграла почти совпадает с его истинным значением. Однако с возрастанием показателя степени оценка (2.13) становится всё более грубой:
……….
и т.д.
При
правая часть в (2.12) уже вдвое больше
левой, а при очень больших значениях
площадь криволинейного треугольника
составляет незначительную часть площади
квадрата. Точный смысл этих рассуждений
выражают равенства
,
(2.14)
Ещё более грубой оценка (2.11) может оказаться в тех случаях, когда функция меняет знак на промежутке .
Пример 2.5. Оценить
интегралы
и
Решение.
Поскольку на отрезке
,
а на отрезке
получаем оценки
Полученные оценки
являются грубыми (рис. 2.15). Далее будет
показано, что
,
Рис. 2.15.
Пример
2.6.
Оценить интеграл
.
Решение.
Нетрудно
убедиться в том, что подынтегральная
функция
убывает на промежутке
и поэтому в силу (2.11) имеем, что
Таким образом, мы выяснили, что значение данного интеграла заключено между числами 0.5 и 0.71. Отметим, что более точные приёмы показывают, что данный интеграл равен 0.62.