2.10. Свойство аддитивности1) интеграла

Если функция интегрируема на отрезке , точка , то имеет место формула

,

(2.5)

т.е. определённый интеграл по всему отрезку равен сумме интегралов по его частям.

Пусть функция неотрицательна на отрезке и . Согласно геометрическому свойству определённого интеграла , , , где - площади под кривой на отрезках соответственно. Поэтому равенство

__________________________________________

(2.5) утверждает наличие следующего очевидного соотношения между этими площадями: .

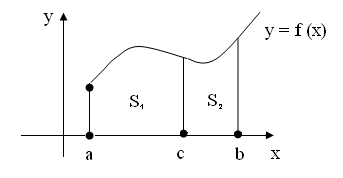
Рис. 2.9

________________________________

¹⁾Аддитивность (от латинского additives – прибавляемый) – свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части. Например, аддитивность площади (объёма) означает, что площадь целой фигуры (целого тела) равна сумме площадей (объёмов) составляющих частей/

Отметим, что соотношение (2.9) справедливо при любом расположении точек . Пусть и функция неотрицательна на отрезке (рис. 2.10). Тогда

.

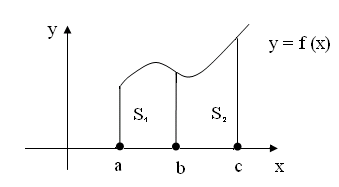
Рис. 2.10

Отсюда следует формула (2.5), утверждающая следующее очевидное соотношение между площадями: , где - площадь под кривой на отрезке .

2.11. Линейные свойства интеграла

Линейные свойства определённого интеграла аналогичны линейным свойствам неопределённого интеграла. В случае неопределённого интеграла эти свойства связаны с линейными свойствами первообразной, в случае определённого интеграла – с линейными свойствами интегральных сумм.

Свойство 2.1. Постоянный множитель можно выносить за знак интеграла, т.к.

,

(2.6)

где - некоторое число.

Пусть фиксированы дробления отрезка и оснащение : дробления .

В силу ассоциативного (распределительного) закона умножения чисел имеем:

.

Переходя в последнем равенстве к пределу при ( - ранг дробления), получим формулу (2.6).

Свойство 2.2. Интеграл от суммы двух функций равен сумме интегралов от этих функций, т.е.

.

(2.7)

Свойство 2.2. доказывается аналогично свойству 2.1.

Нетрудно видеть, что свойство 2.2. остаётся справедливым для любого конечного числа слагаемых функций.

Свойство 2.3. Интеграл от линейной комбинации функций и равен линейной комбинации интегралов от этих функций, т.е.

.

(2.8)

Здесь и - произвольные числа.

2.12. Интеграл от постоянной функции

Если функция постоянна на отрезке , т.е. при любом , то

.

(2.9)

Действительно, при любом оснащении : произвольного дробления отрезка . Поэтому интегральная сумма имеет вид

.

Геометрический смысл формулы (2.9) : интеграл постоянной на отрезке функции равен площади прямоугольника с основанием и высотой (рис. 2.11 ). В частности, при имеем формулу (2.10)

,

(2.10)

т.е. в этом случае интеграл численно совпадает с длиной отрезка .

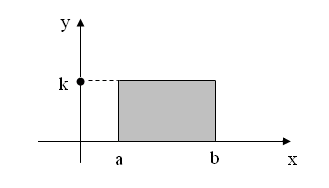
Рис. 2.11