2.8. Проблема существования интеграла
Предел интегральных сумм существуют не всегда. Интегральные суммы, соответствующие данному дроблению при разных его оснащениях, могут значительно отличаться друг от друга и поэтому не быть близкими ни к какому действительному числу.
Пример
2.1. Пусть
- функция Дирихле на отрезке
:
Пусть
- произвольное дробление отрезка
.
Пусть оснащение
состоит из рациональных точек, а
– из иррациональных точек отрезка
.
Тогда все интегральные суммы,
соответствующие оснащению
,
равны 0, а суммы, соответствующие
оснащению
,
равны 1:
Поэтому при
Следовательно,
не существует
предела интегральных сумм в смысле
определения 2.1., т.е. функция Дирихле не
интегрируема
на отрезке
.
Пример
2.2.
Функция
не интегрируема
на отрезке
.
Действительно,
данная функция не
ограничена
на любом отрезке
.
Нетрудно доказать, что для любого сколь
угодно большого числа
и любого дробления отрезка
можно выбрать такое оснащение, что
соответствующая интегральная сумма
превзойдёт
.
Поэтому не
существует конечного
предела
интегральных сумм в смысле определения
2.1.
Отметим, что
геометрически интеграл
представляет собой площадь бесконечно
протяжённой вдоль оси 0Y
плоской фигуры (рис. 2.8). Поэтому вполне
естественно считать эту площадь
бесконечной. В данном случае это
действительно так. Однако, как будет
показано далее (п.2.21) бесконечно
протяжённая плоская фигура может иметь
конечную площадь.
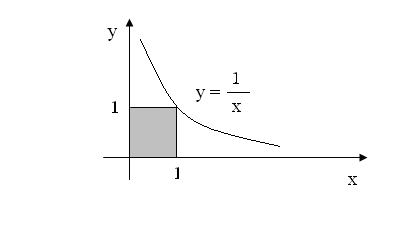
Рис. 2.8.
2.9. Теорема существования определённого интеграла
Приведённые примеры помогают осознать понятие определённого интеграла как предела интегральных сумм и оценить следующую важную теорему.
Теорема 2.1. (Существование определённого интеграла). Если функция непрерывна отрезке , то она интегрируема на этом отрезке, т.е. существует определённый интеграл .
Приведём пример нахождения определённого интеграла на основании определения 2.1.
Пример
2.3.
Вычислить
.
Пусть
– дробление отрезка
с помощью равноотстоящих точек:
Выберем оснащение
:
– совокупность правых концов частичных
отрезков. Составим интегральную сумму
.
Известно, что сумма
квадратов первых
чисел натурального ряда вычисляется
по формуле
-
.(2.4)
Поэтому
.
Отметим, что функция
интегрируема в силу своей непрерывности
(теорема 2.1.). Поэтому выбор дробления и
оснащения не влияет на предел интегральной
суммы.
Приведённый пример показывает, что вычисление определённого интеграла как предела интегральных сумм оказалось возможным благодаря тому, что интегральную сумму удалось привести к виду, удобному для нахождения предела. Такая возможность существует далеко не всегда. Задача интегрирования конкретных функций с помощью определения 2.1 чрезвычайно сложна. Существует эффективный метод вычисления определённых интегралов с помощью так называемой формулы Ньютона-Лейбница, которая будет рассмотрена в п.2. 19.