2.25. Несобственные интегралы

В предыдущих параграфах мы рассматривали интегралы от функций, интегрируемых (и, следовательно, ограниченных) на конечных отрезках интегрирования. На практике возникает необходимость обобщения этих понятий на случаи, когда либо один из концов (или оба) отрезка интегрирования удален в бесконечность, либо функция не ограничена на отрезке интегрирования.

Мы подошли к понятию так называемых несобственных интегралов, использование которых позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры¹⁾.

Рис.2.44

В п 2.7 отмечалось,что площадь бесконечно протяжённой фигуры может быть как бесконечной, так и конечной.

На рисунке 2.44 изображены две бесконечно протяжённые вдоль осей координат криволинейные трапеции, ограниченные гиперболой . Далее будет показано, что площади обеих трапеций бесконечны. В аналогичной ситуации, если вместо гиперболы рассмотреть кривую , то мы увидим далее, что площадь трапеции остаётся бесконечной, а площадь трапеции выражается числом 1.

Различают два вида несобственных интегралов: несобственные интегралы с бесконечными пределами интегрирования и несобственные интегралы от неограниченных функций.

Несобственные интегралы с бесконечными пределами интегрирования

Пусть функция определена и интегрируема на произвольном отрезке , т.е. функция определена для произвольного .

Определение 2.4. Несобственным интегралом от функции на полуинтервале называется предел функции при , стремящемся к , т.е.

.

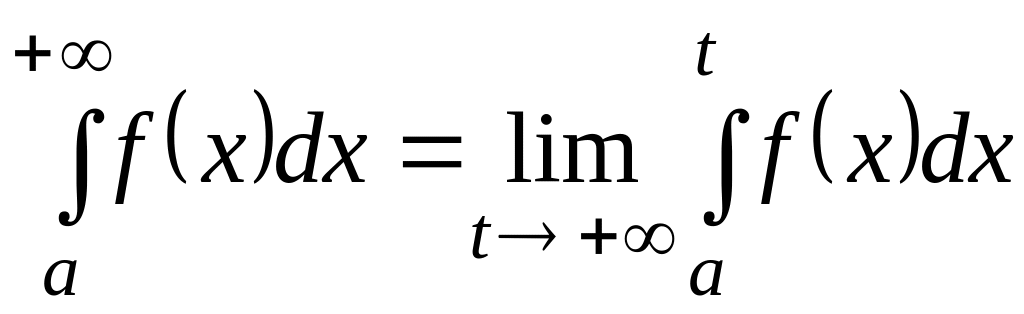(2.32)

Если предел, стоящий в правой части равенства (2.32), существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае - расходящимся.

При работе с несобственными интегралами обычно выделяют следующие две задачи:

а) исследование вопроса о сходимости заданного несобственного интеграла;

б) вычисление значения интеграла в случае, если последний сходится.

В некоторых случаях решения этих двух задач удается объединить.

Пример 2.21. Вычислить .

Решение. По определению .

, ,

т.е. искомый несобственный интеграл сходится к 1. Аналогично, используя формулу Ньютона – Лейбница, можно убедиться, что является сходящимся к , если , и расходящимся, если . Геометрический смысл этого результата состоит в том, что среди всех кривых вида гипербола является своеобразным «порогом»: те кривые данного вида, которые на лежат ниже нее, ограничивают полубесконечную фигуру конечной площади; если же кривая лежит выше или совпадает с гиперболой , то соответствующая фигура имеет бесконечную площадь (рис.2.45).

По аналогии с (2.32) определяется несобственный интеграл на полуинтервале :

.

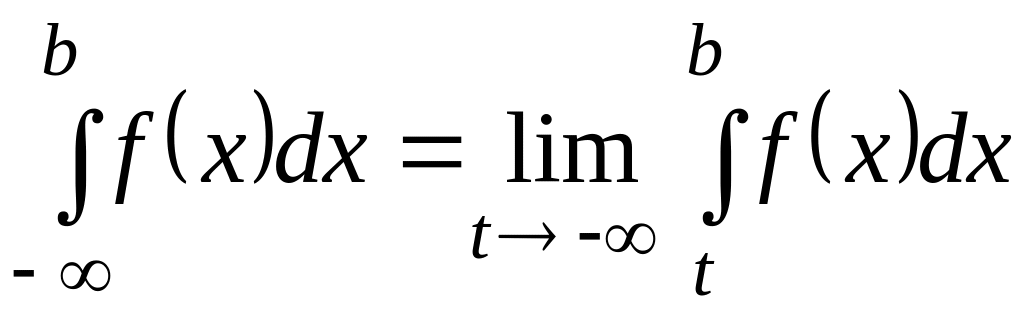(2.33)

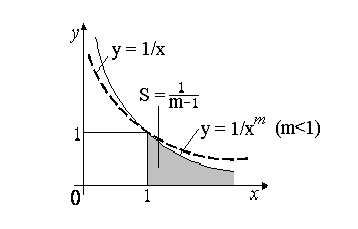
Рис. 2.45

Определение сходимости интеграла аналогично приведенному выше определению 2.4.

Введем понятие несобственного интеграла на интервале . Пусть для некоторого числа несобственные интегралы и сходятся. Тогда положим, что

.

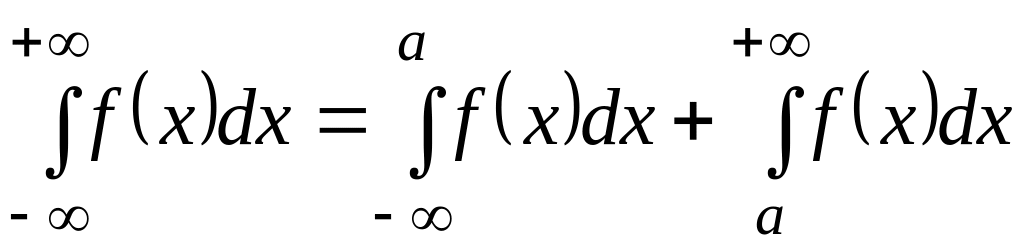(2.34)

При этом интеграл называется сходящимся. Если хотя бы один из интегралов, входящих в правую часть (2.34), расходится, то несобственный интеграл называется расходящимся. (Можно доказать, что введенное определение не зависит от выбора числа ).

Пример 2.22. Вычислить .

Решение. Исследуем на сходимость интегралы и . (В формуле () мы полагаем ).

,

т.е. первый из интегралов сходится к 1. Но

,

т.е. расходится и, поэтому, расходится несобственный интеграл .

Определение 2.5. Интеграл называют интегралом Эйлера – Пуассона.

Справедливо соотношение

(2.35)

В теории вероятностей широко используется функция

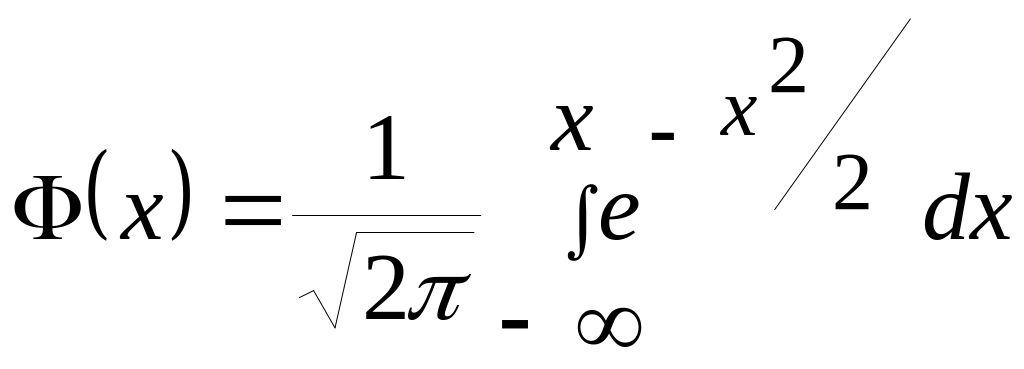, (2.36)

так называемый интеграл вероятности Гаусса.¹⁾

Используя замену переменной и значение интеграла Эйлера – Пуассона, нетрудно убедиться в том, что

, (2.37)

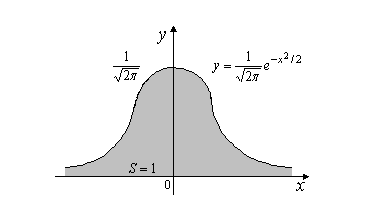Рис. 2.46.

______________________________________

¹⁾Функция является неэлементарной первообразной функции

(см. п.2.11. Неберущиеся интегралы).

другими словами, площадь под кривой (получившей название кривой Гаусса) на интервале равна 1 (рис. 2.46).

Несобственные интегралы от неограниченных функций

Начнем с рассмотрения важного частного случая: пусть функция непрерывна, но не ограничена на полуинтервале .

Определение 2.6. Несобственным интегралом от функции на полуинтервале называется предел , где , т.е.

.

(2.38)

Если предел, стоящий в правой части равенства (2.38), существует и конечен, то несобственный интеграл называется сходящимся, в противном случае - расходящимся.

Аналогично вводится понятие несобственного интеграла от функции непрерывной, но неограниченной на :

.

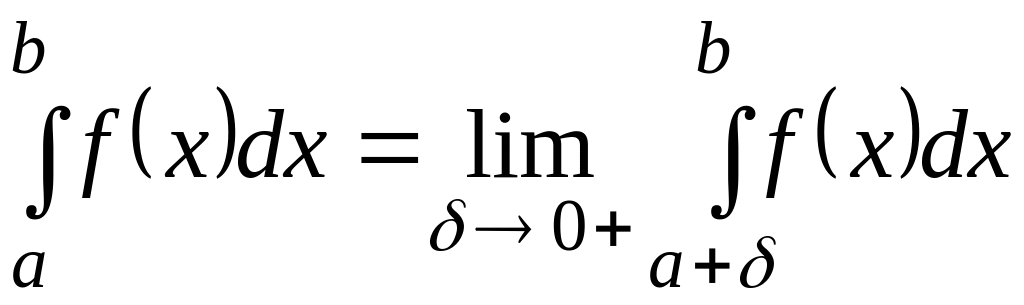(2.39)

Пример 2.23. Вычислить .

Решение. По определению . По формуле Ньютона – Лейбница . Тогда , т.е. полубесконечная фигура, ограниченная осями координат, кривой и прямой , имеет конечную площадь, равную (см. рис. 2.30).

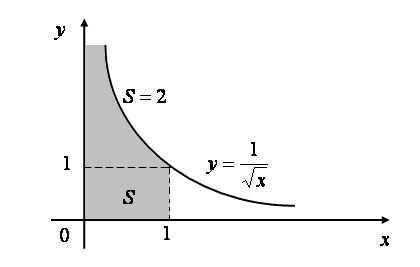
Рис. 2.47.

Замечание 2.7. Если функция имеет бесконечный разрыв в точке , где , то интеграл также называется несобственным. В этом случае интеграл

считается сходящимся, если сходятся два несобственных интеграла в правой части равенства. В противном случае называется расходящимся. Например, является расходящимся, так как расходятся оба несобственных интеграла в правой части равенства (попытайтесь убедиться в этом самостоятельно).