2.24. Определённый интеграл и объёмы тел вращения.
Пусть на отрезке
задана непрерывная знакопостоянная
функция
.
Необходимо найти объем
тела, образованного при вращении вокруг
оси абсцисс криволинейной трапеции,
ограниченной линиями
,
,
,
(рис. 2.35).
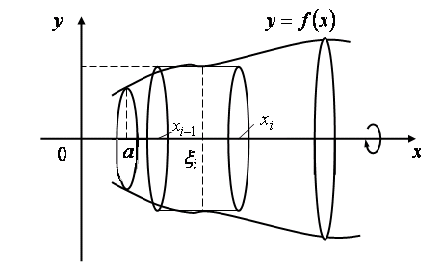
Рис. 2.35
Для решения задачи
применим тот же подход, который был
использован выше для нахождения площади
криволинейной трапеции. Разобьем отрезок
на элементарные отрезки точками:
и на каждом из отрезков разбиения
некоторым образом выберем точку
, где
.
Тогда некоторое приближение для искомого
объема даст следующая сумма
-
,(2.28)
где
,
Геометрический
смысл суммы (2.28) – объём тела, составленного
из цилиндров с радиусами оснований
,
,….,
и высотами
соответственно (рис.2.35). Очевидно,
что приближение для искомого объема
будет тем лучше, чем меньше длины
отрезков разбиения
.
Поэтому за
искомый объем
естественно взять следующий предел
(2.29)
где
- максимальная из длин отрезков разбиения.
Но выражение, состоящее в правой части
(2.29), не что иное, как предел интегральной
суммы для функции
,
поэтому (см. определение 2.1 и формулу
(2.6)) окончательно получаем
(2.30)
Примеры 2.16.
На рисунках
2.36 – 2.38
изображены
плоские геометрические фигуры:
прямоугольник, треугольник и полукруг.
В результате вращения этих фигур вокруг
оси
получаются объёмные фигуры -– цилиндр,
конус и шар соответственно. Вычислим
объёмы этих тел с помощью формулы (2.
30)
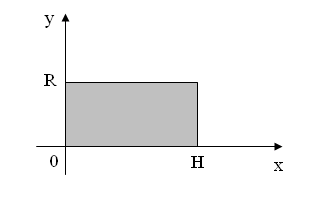Рис.
2.36.
,
Напомним формулы
стереометрии.
– объём цилиндра (
– радиус основания,
– высота цилиндра);
– объём конуса (
– радиус основания,
– высота конуса);
– объём шара.
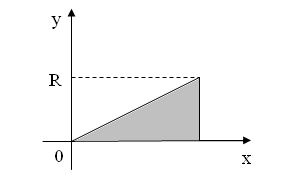Рис.2.37.
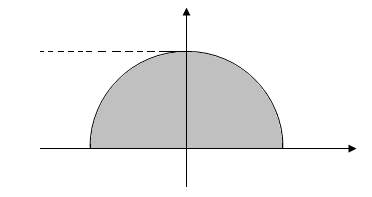
Рис. 2.38
Пример
2.17.
Вычислить
объем тела, полученного от вращения
фигуры, ограниченной линиями
,
,
,
вокруг оси
.
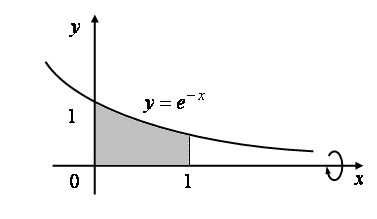
Рис. 2.39
Решение. По формуле (2.30) искомый объем
.
Пример
2.18.
Вычислить
объем тела, полученного при вращении
вокруг оси
фигуры, ограниченной осью
и одной аркой синусоиды (рис. 2.40).
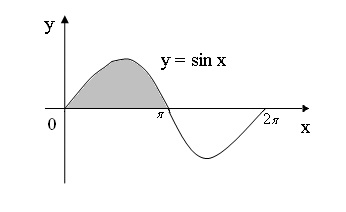
Рис. 2.40.
Решение.
Поскольку функция
является
-периодической,
для вычисления нужного объёма достаточно
рассмотреть её на отрезке
Формально заменяя
в формуле (2.30) переменную
на
получаем
формулу для вычисления объёма
тела, полученного при вращении
криволинейной трапеции вокруг оси
ординат:
(2.31)
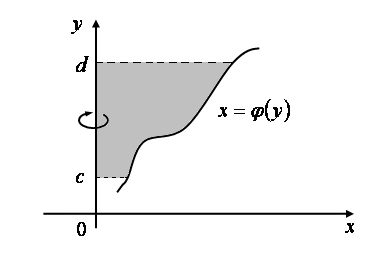
Рис. 2.41.
Пример
2.19. Найти объём тела,
полученного при вращении вокруг оси
ординат фигуры, ограниченной линиями:
,
,
(рис. 2.39).
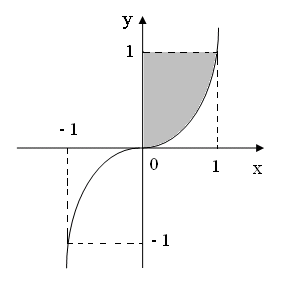
Рис.2.42.
Решение. Применяя формулу (2.31), получаем
Пример
2.20.
Найти
объем тела, полученного от вращения
вокруг оси ординат плоской фигуры,
ограниченной линиями
,
.
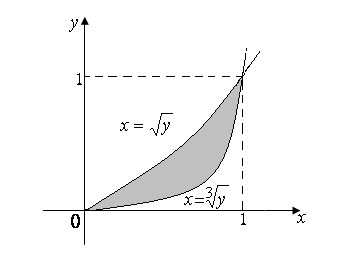
Рис.2.43.
Решение.
Проецируя
вращаемую фигуру на ось ординат
(рис.2.43), убеждаемся, что искомый
равен разности двух объемов: объема
,
полученного от вращения вокруг оси
ординат фигуры, ограниченной линиями
,
,
,
и объема
,
для которого вращаемая фигура ограничена
линиями
,
,
.
(С учетом предстоящего применения
формулы (2.31) уравнения кривых записаны
в виде
,
предполагающем переменную
независимой). Применяя (2.31), получаем:
,
.
Окончательно
.