78

Глава 2. Определённый интеграл

2.1. Задача о площади криволинейной трапеции

Пусть на отрезке задана неотрицательная функция . Требуется найти площадь под кривой на отрезке - площадь криволинейной трапеции, ограниченной кривой , прямыми и осью абсцисс (рис.2.1.).

Рис. 2.1 Рис. 2.2

Наметим общий подход к решению этой задачи. Построим ломаную, достаточно близко расположенную к кривой на (рис. 2.2.). Фигура под ломаной состоит из трапеций и прямоугольников, её площадь может быть вычислена с помощью известных формул планиметрии. Поскольку ломаная выбрана достаточно близко к кривой , имеем приближённое равенство .

Это равенство оказывается тем более точным, чем ближе расположена ломаная к исходной кривой. Поэтому за искомую площадь можно принять предел переменной площади под ломаной в предположении неограниченного приближения ломаной к кривой.

Приведённые рассуждения носят качественный характер. Для того, чтобы их можно было использовать на практике, необходимо дать строгое описание процедуры выбора ломаной и последующую предельного перехода. На этом пути мы придём к понятию определённого интеграла.

2.2. Интегральные суммы

Пусть функция определена на отрезке . Пусть - упорядоченная совокупность точек отрезка :

.

Точки разбивают (дробят) отрезок на произвольных частей. Назовём такое разбиение отрезка дроблением , точки будем называть точками дробления .

Обозначим через - длину частичного отрезка

Выберем на каждом частичном отрезке произвольную точку . Совокупность точек назовём оснащением дробления . Отметим, что всякое дробление имеет бесконечно много оснащений.

Составим сумму

Сумму называют интегральной суммой для функции на отрезке . Итак,

Интегральная сумма данной функции на данном отрезке зависит от дробления , число точек которого может быть сколь угодно большим, и от выбора оснащения .

2.3. Геометрический смысл интегральной суммы

В случае, когда функция неотрицательна на отрезке , интегральная сумма имеет простой геометрический смысл: она совпадает с площадью ступенчатой фигуры, составленной из прямоугольников с основаниями и высотами соответственно. Верхняя граница ступенчатой фигуры – ломаная с горизонтальными звеньями, которая в той или иной степени приближает кривую (см. п.1.1).

Отметим, что вообще говоря, расстояние между соседними точками дробления являются различными.

На рисунке 2.3 изображено дробление отрезка с помощью равноотстоящих точек. Ему соответствует оснащение из середин частичных отрезков.

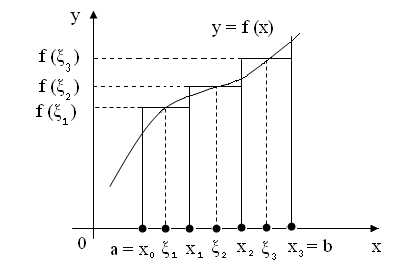
Рис. 2.3

2.4. Ранг дробления

Рангом дробления назовём длину наибольшего частичного отрезка:

.

Если дробление очень мелкое, т.е. если число очень мало, то число точек этого дробления велико. Обратное неверно: дробление, содержащее много точек, не обязано быть мелким (рис. 2.4).

Рис. 2.4