Тема 7. Двумерные случайные величины Теоретические сведения
Двумерной случайной величиной ( , ) называется совокупность (система) двух случайных величин. Геометрически ее можно интерпретировать как случайную точку на плоскости.
Функция
распределения двумерной случайной
величины:
.
Свойства функции распределения:
1.
;
2.
;
3.
,
и
– функции распределения случайных
величин
и
соответственно;
4.
– неубывающая функция х
и у.
Вероятность попадания точки ( ,) в прямоугольник R со сторонами, параллельными осям координат:
Плотность
распределения двумерной
случайной величины
выражается через функцию распределения:
.
Свойства плотности распределения:
1.
;
2.
.
Вероятность попадания точки (x ,h) в произвольную область D:
Функция распределения двумерной случайной величины выражается через плотность:
.
Плотности распределения отдельных компонент:
;
Условные плотности распределения:
.
Для расчета начальных и центральных моментов используются формулы:
;
.
Ковариация
характеризует
рассеяние и зависимость случайных
величин:
.
Коэффициент корреляции:
.
Всегда
.
Упражнения
Два стрелка независимо один от другого производят по одному выстрелу, каждый по своей мишени. Случайная величина – число попаданий первого стрелка, – второго стрелка. Вероятность попадания в мишень для первого стрелка равна 0.7, для второго – 0.8. Построить функцию распределения двумерной случайной величины ( , ).
По мишени производится один выстрел. Вероятность попадания равна 0.75. Рассматриваются две случайные величины: – число попаданий; – число промахов. Построить функцию распределения двумерной случайной величины ( , ).
Имеются две независимые случайные величины. – распределена по показательному закону с параметром , а – по показательному закону с параметром . Написать выражения для плотности распределения и функции распределения двумерной случайной величины ( , ).
Двумерная случайная величина ( , ) распределена с постоянной плотностью внутри квадрата со стороной 1. Написать выражение для плотности распределения
.
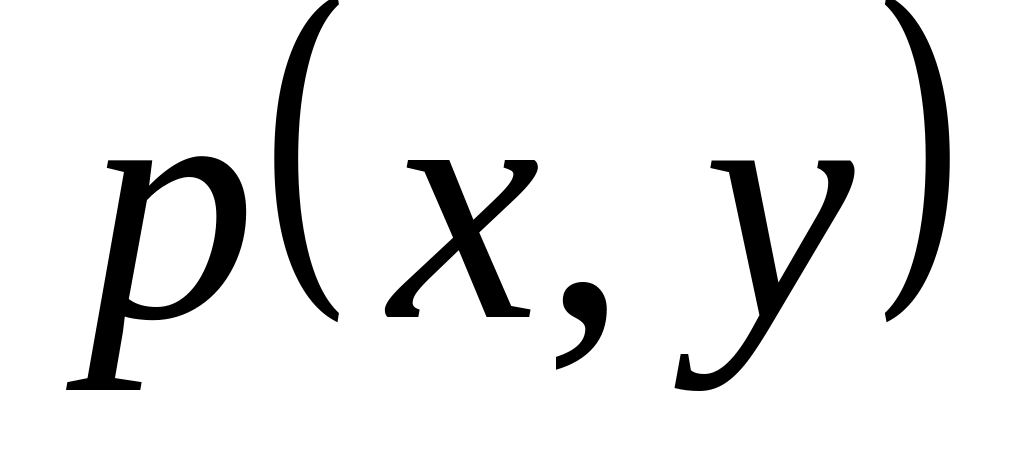Построить функцию распределения
.
Написать выражения для плотностей
компонент. Определить, являются ли
случайные величины
и
независимыми или зависимыми.Найти вероятность попадания случайной точки ( , ) в прямоугольник, ограниченный прямыми:
,
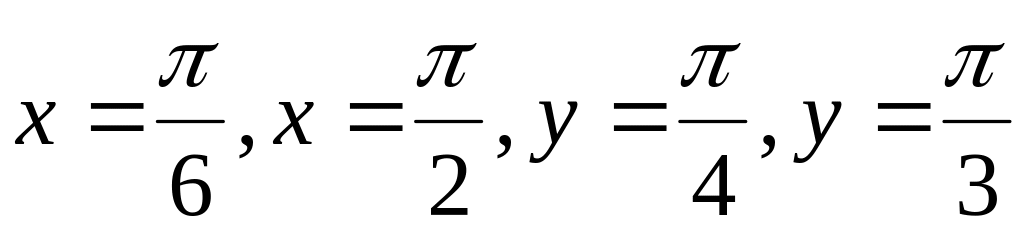если известна функция распределения
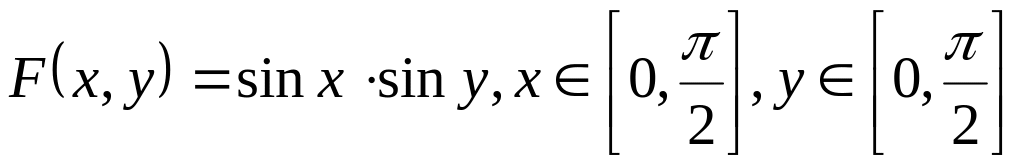.Найти плотность совместного распределения случайной величины (, ) по известной функции распределения
.Найти функцию распределения случайной величины ( , ) по известной плотности совместного распределения:
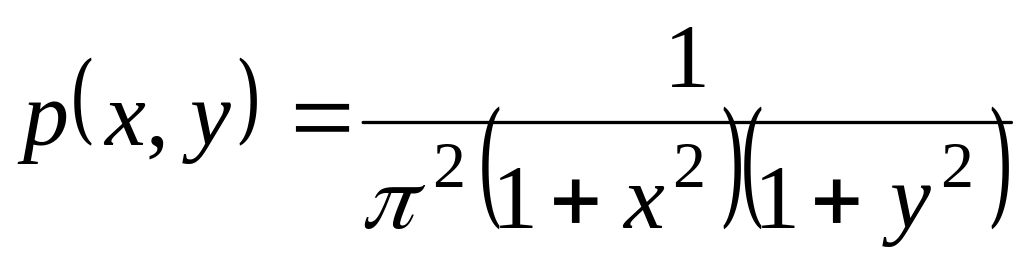.Двумерная случайная величина ( , ) задана плотностью совместного распределения:
.
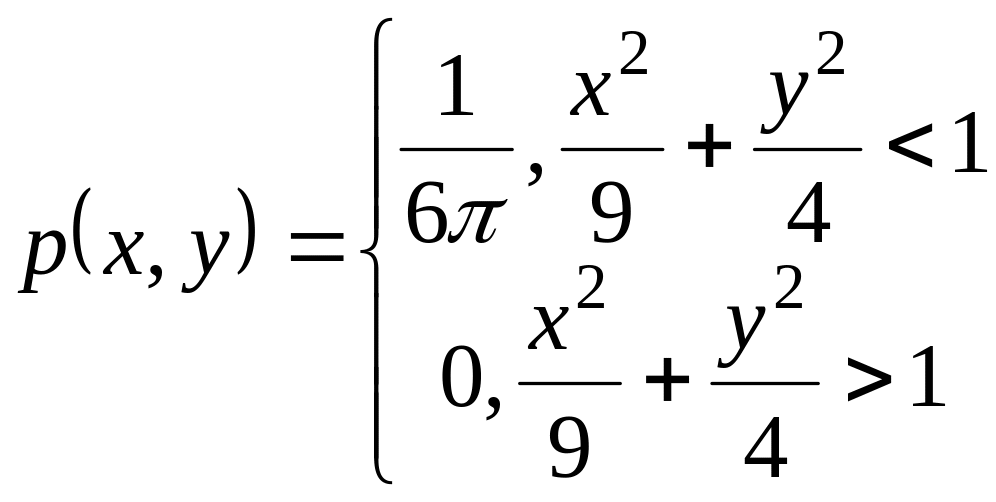Найти плотности распределения
составляющих
и .
Показать, что
и
зависимые некоррелированные величины.Двумерная случайная величина ( , ) задана плотностью совместного распределения:
.
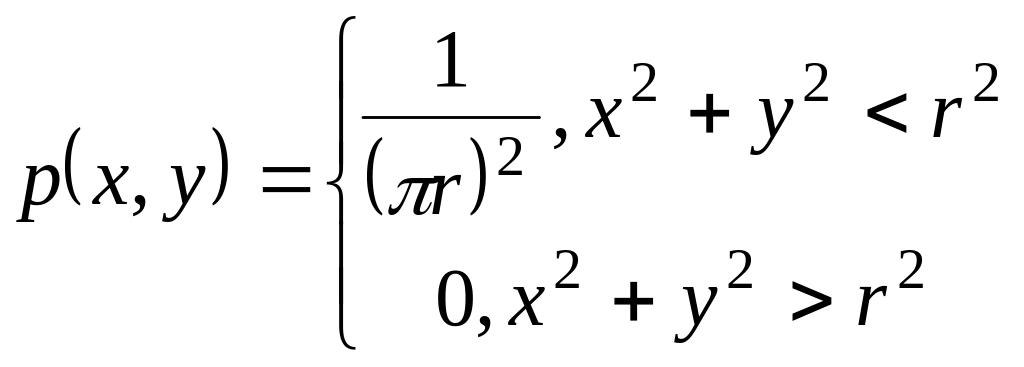Найти условные законы распределения
составляющих
и .