45) Интегрирование тригонометрических функций

1°. Интегралы вида

находятся с помощью тригонометрических формул

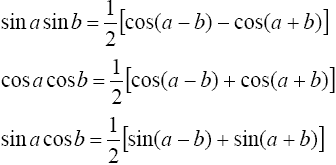
2°. Интегралы вида

где m и n - четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

3°. Если m = -, n = - - целые отрицательные числа одинаковой четности, то

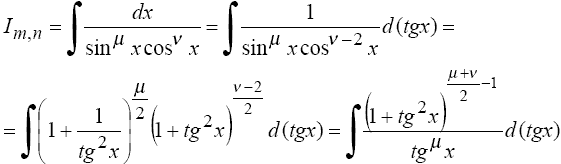
В частности, к этому случаю сводятся интегралы

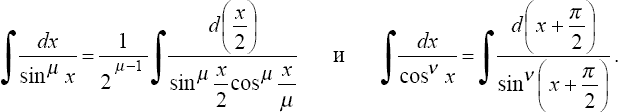4°. Интегралы вида

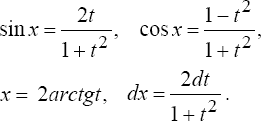где R - рациональная функция от sinx и cosx, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки при этом Если R{-sin x, cosx) = R(sinx, cosx), то целесообразно применить подстановку tgx = t. при этом

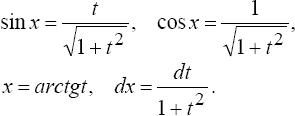
46) Интегрирование некоторых иррациональных функций

Не от всякой иррациональной функции интеграл выражается через элементарные функции. Рассмотрим те функции, интегралы от которых с помощью подстановок приводятся к интегралам от рациональных функций и интегрируются в элементарных функциях.

1) Если под знаком интеграла стоит рациональная функция от дробных степеней независимой переменной  , т. е. рассматривается , то подынтегральная функция преобразуется в рациональную функцию от   с помощью подстановки  , где   - общий знаменатель дробей  :  ,  .

2) Если под знаком интеграла стоит рациональная функция от дробных степеней выражения  , т. е.  ,то с помощью подстановки  , где   - общий знаменатель дробей  , подынтегральная функция преобразуется в рациональную дробь. Для нахождения   выполним преобразования: выразим  ,   и  .

3) Рассмотрим теперь интеграл вида  .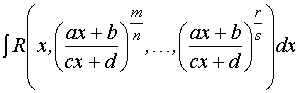

Этот интеграл сводится к интегралу от рациональной функции с помощью подстановки  , где   - общий знаменатель дробей  . Для нахождения   необходимо предварительно выразить   из равенства  . Поясним на примере.

Интегрирование дифференциальных биномов.

Выражение вида   называется дифференциальным биномом, где   - любые постоянные, а показатели   - рациональные числа. Выясним случаи, когда эти выражения интегрируются в конечном виде.

Один такой случай ясен непосредственно: если   - число целое, то рассматриваемое выражение относится к типу, изученному в пункте 3.5. Именно, если через   обозначить наименьшее общее кратное знаменателей дробей  , то мы имеем здесь выражение вида  , для рационализации которого достаточна подстановка  . Преобразуем теперь данное выражение подстановкой  . Тогда

Пусть  , тогда будем иметь

 (3.2)

Если   - целое число, то вновь переходим к выражению изученного вида. Действительно, если обозначить через   знаменатель дроби  , то преобразованное выражение имеет вид  . Рационализации подынтегрального выражения можно достигнуть подстановкой  .

 Наконец, перепишем второй из интегралов (3.2) так:

Если   - целое число, то также имеем изученный случай: преобразованное выражение имеет вид  , которое рационализируется подстановкой  .

Таким образом, оба интеграла (3.2)выражаются в конечном виде, если оказывается целым одно из чисел  ,  ,  .

Эти случаи интегрируемости были известны еще Ньютону. Однако, лишь в середине XIX в. Чебышев установил замечательный факт, что других случаев интегрируемости в конечном виде для дифференциальных биномов нет. Рассмотрим примеры.

Интегрирование выражений вида  . 

Подстановки Эйлера

Переходим к рассмотрению очень важного класса интегралов  .

Предполагаем, что квадратный трехчлен не имеет равных корней, так что корень из него не может быть заменен рациональным выражением. Изучим три подстановки, называемые подстановками Эйлера, с помощью которых можно достигнуть здесь рационализации подынтегрального выражения.

1 подстановка применима в случае, если  . Тогда полагаем,   (можно было бы положить и  ).

Возводя это равенство в квадрат, находим  .

Отсюда  ,  ,  .

Если полученные выражения подставить в подынтегральное выражение, то вопрос сведется к интегрированию рациональной функции от  . В результате, возвращаясь к  , нужно будет положить  .

2 подстановка применима, если  . В этом случае полагаем   (или  ).

Если возвести в квадрат, уничтожить   в обеих частях и сократить на  , то получим   - уравнение первой степени относительно  . Отсюда

;  ;

.

Подставив это в подынтегральное выражение, придем к рациональной функции. Проинтегрировав, в результате положим

.