26. Выпуклость и вогнутость кривой.

Определение. Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.

Определение.

Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Опр. Пусть на плоскости xy имеется график функции y=f(x) на [a,b], говорят что кривая обращена выпуклостью вверх, если все точки этой кривой лежат ниже любой касательной к этой кривой.

Кривая обращена выпуклостью вниз, если любая его точка лежит выше любой касательной кривой.

Если во всех точках интервала а,в вторая производная функции f’’(x)<0(f’’(x)>0), то кривая на этом интервале выпукла (вогнута)

Опр. Точка, определяющая выпуклую часть кривой от вогнутой наз. Точкой перегиба

Пусть кривая определена y=f(x), если вторая производная f’’(x)=0 или не существует и при переходе через эту точку вторая производная меняет знак, то эта точка есть точка перегиба. Точка называется точкой перегиба графика функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости. Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

27 Асимптоты кривой

Очень часто приходится исследовать поведение ф-и при стремлении х или у или обоих к бесконеч.

Опр. Прямая А называется асимптотой кривой y=f(x), если расстояние между ними стремится к 0 при х стрем к бесконеч, У стремящемся к бесконеч.

28 Функции нескольких переменных

Опр. Если каждой паре независимых переменных ( х,у) из области их определения соответствует по определенному закону некоторое значение переменной z, то говорят задана функция от 2-х независимых переменных и записывется в виде z=f(x,y), x=F(x,y) примера нет

Переменная величина u называется функцией многих переменных, например, от двух x и y, если каждой рассматриваемой совокупности значений величин и (допустимые значения) соответствует одно определенное значение величины u.

Здесь переменные x и y называются независимыми переменными или аргументами, совокупность рассматриваемых их значений называется областью определения или областью существования функции u.

То есть факт, что u есть функция от x и y обычно записывается так

u = f (x, y.)

29.Частные и полные приращения

Частные приращения функции 2-х переменных. Разность = f (x+?x, y) – f (x, y) называется частным приращением функции f (x, y) по переменной x. Разность = f (x, y+?y) – f (x, y) называется частным приращением функции f (x, y) по переменной y. ПОЛНОЕ ПРИРАЩЕНИЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФНП

Полным приращением функции двух переменных   в точке   называется выражение  .

Предположим, что в точке   и некоторой ее окрестности функция z = f(x,y) имеет непрерывные частные производные первого порядка   и  . Выразим через них полное приращение  :

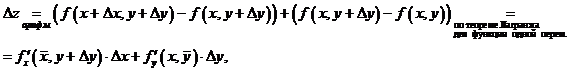 (1) где  заключено между   и  ,   заключено между   и 

Функция z = f (x, y), полное приращение Dz которой в данной точке (x, y) может быть представлено в виде суммы двух слагаемых: выражения, линейного относительно    и  , и величины, бесконечно малой более высокого порядка малости относительно  , называется дифференцируемой ФНП в данной точке, а линейная часть ее полного приращения называется полным дифференциалом ФНП.