16. Формула Тейлора

17-19 Разложение функции e^x

Так как (e^x)' = e^x, то производная любого порядка функции e^x равна e^x. При x = 0 функцияe^x и ее производные любого порядка равны одному. Таким образом, формула Маклорена для функции e^x имеет вид

Отметим, что для любого вещественного числа x остаточный член

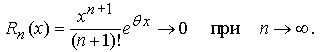
В самом деле, если x – фиксированное число, то, начиная с некоторого положительного целого числа N, для любого n > N имеем

Следовательно

так как q < 1, а величина 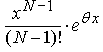  является постоянной при любом n. Таким образом, значения функции e^x могут быть найдены приближенно по формуле:

Разложение функции cos x

Находим последовательно производные от f(x) = cos x.

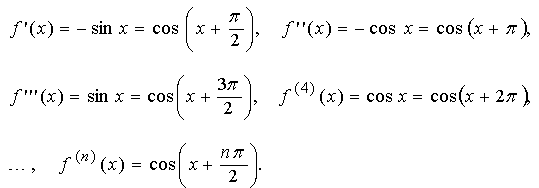
При x = 0 получаем

Следовательно, формула Маклорена для функции cos x имеет вид

Так как  , то

для любого фиксированного вещественного числа x. Таким образом, значения функцииcosx могут быть найдены приближенно по формуле

Разложение функции sin x

Формула Маклорена для функции sin x находится аналогично формуле Маклорена для cos x

Причем

для любого фиксированного вещественного числа x.

20) Исследование функции с помощью производных. 1. Если производная на некотором отрезке больше нуля, то на этом отрезке функция возрастает. 2. Если производная на некотором отрезке меньше нуля, то на этом отрезке функция убывает. 3. Точки, где производная равна нулю или не существует являются критическими точками. В этих точках может быть экстремум функции(то есть максимумы и минимумы). Для их нахождения поступают так: 1) Распологают на координатной прямой критические точки. 2) Внутри каждого промежутка(промежуток знакопостоянства) для произвольной точки найти знак первой производной. 3) Если знак в соседних интервалах разный, екстремум есть, иначе нет. Там, где знак меняется с плюса на минус, будет максимум(не путать с максимальным значением). Там, где знак меняется с минуса на плюс, будет минимум(не путать с минимальным значением). Максимум и минимум можно определить и по второй производной(если она существует). Там, где вторая производная в точке екстремума больше нуля – минимум. Там, где вторая производная в точке екстремума меньше нуля – максимум. 4. Точки, где вторая производная равна нулю или не существует являются критическими точками для нахождения точек перегиба то есть таких точек, где функция меняет вогнутьсть на выпуклость и наоборот. Критические точки разбивают область определения функции на интервалы. В том интервале, где вторая производная больше нуля, функция вогнута. В том интервале, где вторая производная меньше нуля, функция выпукла.

Определение. Функция   называется возрастающей в точке   , если в некоторой   -окрестности этой точки справедливо

для любого   .

Определение. Функция   называется возрастающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .

Определение. Функция   называется убывающей в точке   , если в некоторой   -окрестности этой точки справедливо неравенство

для любого   .

Определение. Функция   называется убывающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .

Определение. Функция   имеет в точке   максимум, если значение   является наибольшим в некоторой двустороней окрестности точки   .

Определение. Функция   имеет в точке   минимум, если значение   является наименьшим в некоторой двусторонней окрестности точки   .

Определение. Функция   имеет в точке   экстремум, если точка   является точкоймаксимума или минимума.

Признаки (достаточные) возрастания и убывания функции   :

Если   на интервале   , то функция   возрастает на этом интервале;

Если   на интервале   , то функция   убывает на этом интервале.

21) МАКСИМУМ И МИНИМУМ ФУНКЦИИ наибольшее и соответственно наименьшее значения функции, принимающей действительные значения. Точку области определения рассматриваемой функции, в к-рой она принимает максимум или минимум, наз. соответственно точкой максимума или точкой минимума (см.Максимума и минимума точки).Если нек-рая точка является точкой абсолютного (локального) максимума или минимума, строгого или нестрогого, то значение функции в этой точке наз. абсолютным (локальным), соответственно строгим или нестрогим максимумом или минимумом. Если функция непрерывна на компакте, то она всегда принимает на нем максимальное и минимальное значения.