1.9. Метод эквивалентного преобразования схем

В ряде случаев расчет сложной электрической цепи упрощается, если в ее схеме замещения заменить группу резистивных элементов другой эквивалентной группой, в которой резистивные элементы соединены иначе. Взаимная эквивалентность заключается в том, что после замены режим работы остальной части цепи не изменится.

А. Смешанное соединение резистивных элементов. При наличии в цепи одного источника внешнюю по отношению к нему части схемы можно в большинстве случаев рассматривать как смешанное (после­довательно-параллельное) соединение резистивных элементов.

Для расчета такой цепи удобно преобразовать ее схему замещения в эквивалентную схему с последовательным соединением резистив­ных элементов. Например, в цепи на рис. 1.14, а между узлами а и b включены три резистивных элемента с сопротивлениями и , т. е. проводимостями g₂=1/ , g₃=1/ , g₄=1/ ; эквивалентная проводимость

. (1.15)

После замены параллельного соединения резистивных элементов эквивалентным резистивным элементом с сопротивлением получается эквивалентная схема с последовательным соединением двух резистивных элементов r₁ и (рис. 1.14,6).

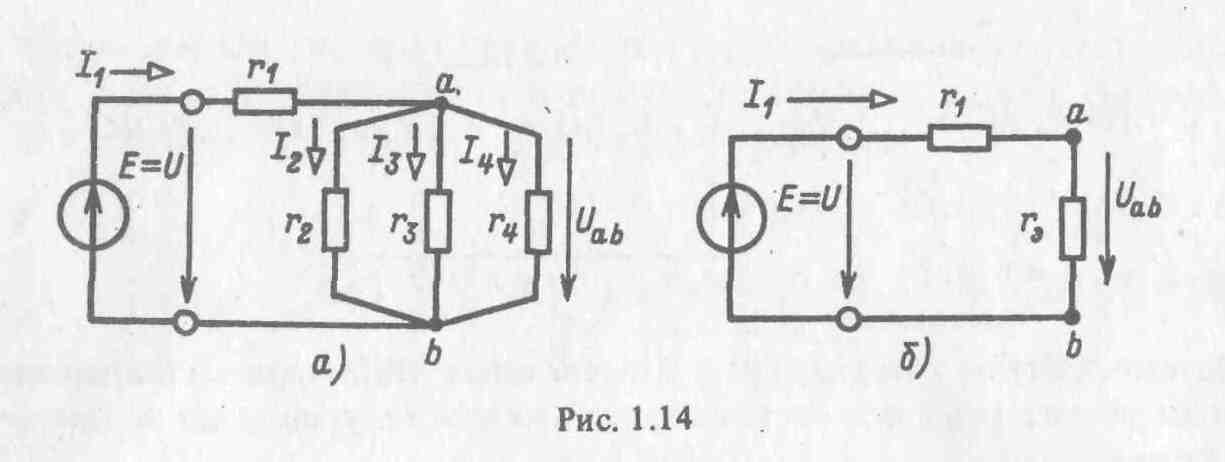
Рис. 1.14

Ток в неразветвленной части

и токи в параллельных ветвях

(1.16)

где

.

Б. Соединение резистивных элементов по схеме звезды и треуголь­ника. В общем случае схему замещения цепи по схеме n-лучевой звез­ды из резистивных элементов можно заменить эквивалентной схемой в виде n-стороннего многоугольника. Обратное преобразование воз­можно в ограниченном числе случаев. В частности, преобразования в обоих направлениях возможны для случая треугольника и трех­лучевой звезды. Такое преобразование применяется при расчетах слож­ных цепей постоянного тока и цепей трехфазного тока (см. гл. 3).

Эквивалентность схем в виде треугольника и звезды (рис. 1.15) получается приравниванием значений сопротивлений или проводимостей между одноименными узлами этих схем, отсоединенных от остальной части цепи.

Найдем сопротивление между узлами А и В.

Проводимость между узлами А и В для схемы треугольника на рис. 1.15, а

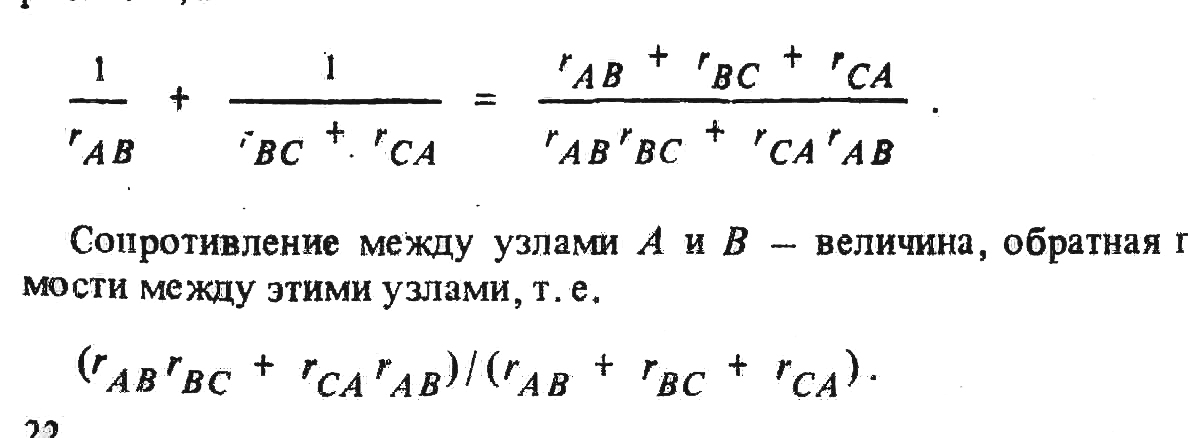
Сопротивление между узлами А и В – величина, обратная проводи­мости между этими узлами, т. е.

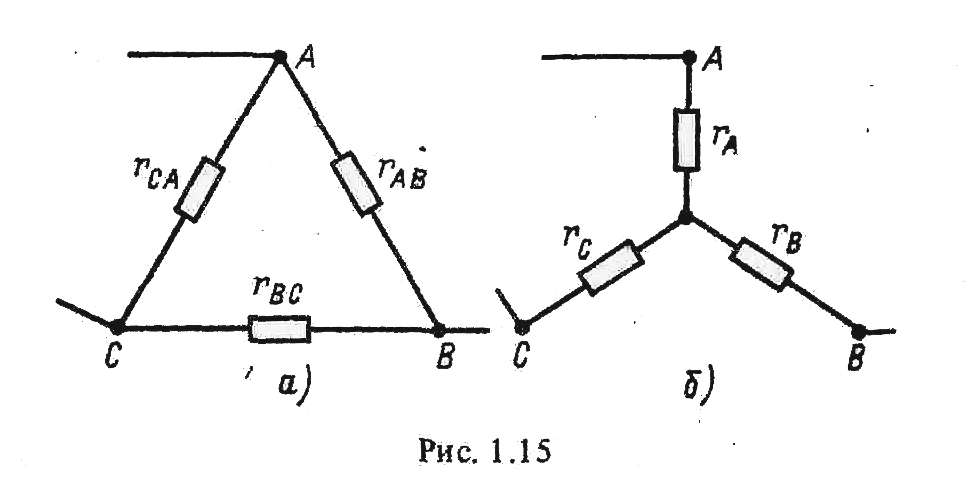
Рис.1.15.

Для схемы звезда на рис. 1.15,б сопротивление между теми же уз­лами А и В равно сумме сопротивлений двух ветвей: .

Согласно условию эквивалентности должно выполняться равенство

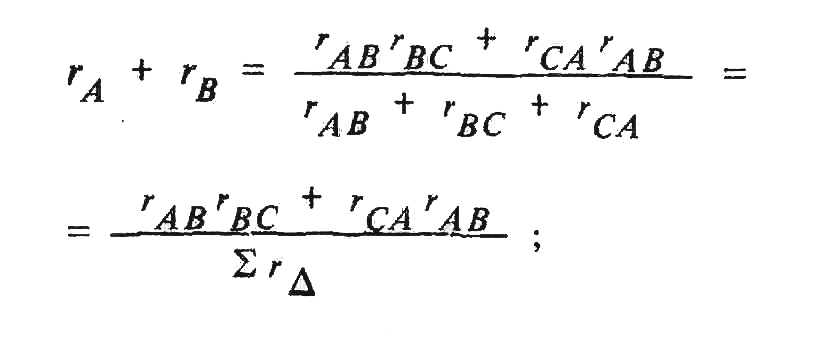(1.17)

здесь –сумма сопротивлений всех ветвей для треугольника.

Структуры треугольника и звезды по отношению к узлам симмет­ричны. Поэтому уравнения равенства сопротивлений между узлами В и С и между узлами С и А можно получить из (1.17) простой цикли­ческой перестановкой индексов:

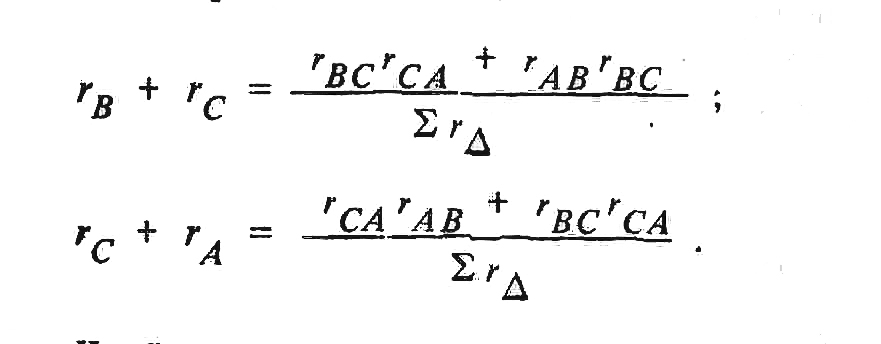(1.18)

(1.19)

Чтобы определить сопротивление r_А звезды, сложим (1.17) и (1.19) и вычтем из этой суммы (1.18); разделив последнее на 2, найдем

(1.20)

Сопротивления других ветвей звезды получим путем циклической перестановки индексов:

(1.21)

(1.22)

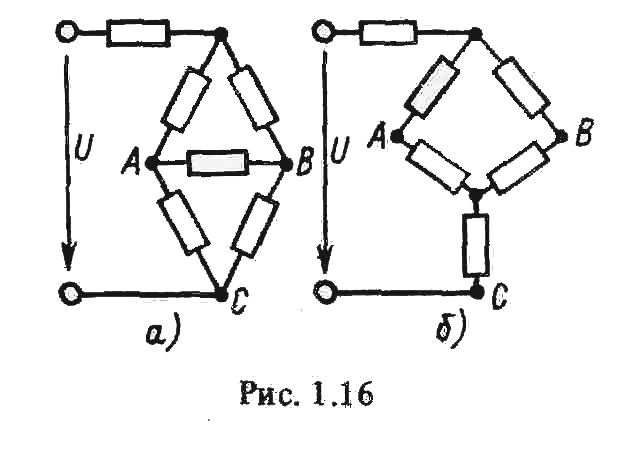
Рис. 1.16

В случае равенства сопротивлений ветвей треугольника ( ) сопротивления ветвей эквивалентной звезды тоже одина­ковы:

. (1.23)

Возможно обратное преобразова­ние звезды из резистивных элемен­тов в эквивалентный треугольник. Для этого перемножим попарно выражения (1.20)–(1.22) и сло­жим полученные произведения:

Последнее уравнение разделим на (1.22) и определим сопротивление ветви треугольника:

(1.24)

Путем циклической перестановки индексов в (1.24) найдем выра­жения для сопротивлений двух других ветвей:

(1.25)

(1.26)

Примером упрощения расчетов может служить преобразование мосто­вой схемы соединения резистивных элементов (рис. 1.16, а). После за­мены одного из треугольников эквивалентной звездой всю цепь (рис. 1.16, б) можно рассматривать как смешанное соединение резистивных элементов.