Построение

При построении B+ дерева, его временами приходится перестраивать. Это связано с тем, что количество ключей в каждом узле (кроме корня) должно быть от k до 2k, где k — степень дерева. При попытке вставить в узел (2k+1)-й ключ возникает необходимость разделить этот узел. В качестве ключа-разделителя сформированных ветвей выступает (k+1)-й ключ, который помещается на соседний ярус дерева. Особым же случаем является разделение корня, так как в этом случае увеличивается число ярусов дерева. Особенностью разделения листа B+ дерева является то, что он делится на неравные части. При разделении внутреннего узла или корня возникают узлы с равным числом ключей k. Разделение листа может вызвать «цепную реакцию» деления узлов, заканчивающуюся в корне.

Свойства

• В B+ дереве легко реализуется независимость программы от структуры информационной записи.

• Поиск обязательно заканчивается в листе.

• Удаление ключа имеет преимущество — удаление всегда происходит из листа.

• Другие операции выполняются аналогично B-деревьям.

• B+ деревья требуют больше памяти для представления чем B-деревья.

• B+ деревья имеют возможность последовательного доступа к ключам.

Инвертированные спискипозволяют существенно ускорить процесс поиска необходимой информации по сравнению с линейными списками. Это достигается с помощью упорядочивания (сортировки) записей исходного списка по значениям данных в одном из неключевых полей. Инвертирование исходного списка можно выполнить для отдельных (частичное инвертирование) или всех (полное инвертирование) неключевых полей исходного списка.

Связный список - это разновидность линейных структур данных, представляющая собой последовательность элементов, обычно отсортированную в соответствии с заданным правилом. Последовательность может содержать любое количество элементов, поскольку при создании списка используется динамическое распределение памяти. Каждый элемент связного списка представляет собой отдельный объект, содержащий поле для хранения информации и указатель на следующий элемент списка (а в случае двусвязного списка в объекте хранится также указатель на предыдущий элемент). 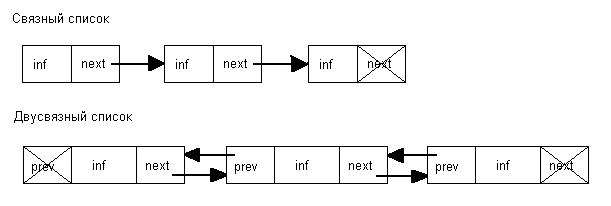Схема, изображающая связный и двусвязный списки из трех элементов: Передвижение по списку осуществляется по указателям, которые указывают на соседние элементы списка. При добавлении нового элемента к списку необходимо динамически выделить под него память и присвоить соответствующие значения указателям соседних элементов, а также указателям самого созданного элемента.