11

Сигналдар және сызықты системалар

Signals and linear systems. Discrete transformations of signals.

Тақырып 8. СИГНАЛДАРДЫҢ ДИСКРЕТТІ ТҮРЛЕНУІ

Нет ничего, сколь бы великим и изумительным оно не показалось с первого взгляда, на что мало-помалу не начинаешь смотреть с меньшим изумлением.

Лукреций. Римский поэт и философ, I в.д.н.э.

Преобразование должно быть осознанным и целенаправленным действом. Был баран - стал шашлык. Что может быть прекраснее такого преобразования!

Виль Ибрагимов. Ташкентский геофизик Уральской школы, ХХ в.

Мазмұны

1. Фурье түрленуі.Дискретті Фурье түрленуі. Тез Фурье түрленуі

2. Лаплас түрленуі.

3. Z –сигнал түрленуі. Түрлену түсінігі. z- түрлену мысалдар.Фурье және Лаплас түрленулердің байланысы. z- түрленудің қасиеттері.z- түрлену бейнесі. Аналитическая форма z-образдардың аналитикалық формасы. z- кері түрленуі.

4. Дискретті свертка (конволюция). Дискретті свертка теңдеуі. Свертка техникасы.

кіріспе

Сигналдардың цифрлі өңдеуі дискретті сигналдардың өзгеруіне қатысты және өзгерілетін сигналдар система деректеріне.Дискреттілердің өзгеруінің математикасы 18 ғасырдың аналогты математикасында қатарлар теориясының шеңберінде туды және олардың функциясының интерполяция және аппроксимациянда қолданылады,бірақ дамудың тездетуі н 20 ғасырда алды ең алғышқы есептегіш машиналар пайда болғанда.Негізі , дискретті өзгертудің математикалық аппараты аналогты сигналдардың және ситсемалардың түрленуніне ұқсас.Бірақ берілгендердің дискреттілігі факторлардың санауын қажет етеді, және елемеушілік маңызды қателерге әкеледі.Сонымен қоса , әдістер қатары дискретті математикада аналогтарға ие емес аналатикалық математикада.

8.1. Фурье түрленуі [5,17,21].

Дискретті Фурье түрленуі аргументтің дискретизация интегралының түрленуімен тікелей алынуы мүмкін (t_k = kt, f_n = nf):

S(f) = s(t) exp(-j2ft) dt, S(f_n) = t s(t_k) exp(-j2f_nkt), (8.1.1)

s(t) = S(f) exp(j2ft) df, s(t_k) = f S(f_n) exp(j2nft_k). (8.1.2)

Еске түсірейк , уақыт бойынша дискретизация функциясы спектрдің периодтылығынна алып келеді,ал жиілік бойынша спектрдің дискретизацисы – функция периодтылығына алып келеді. Сонымен қоса ұмытпауымыз керек (8.1.1) сандық қатардың S(f_n)-ы функцияның үзіліссіз дискретизация S'(f) функцияның дискретті спектрі s(t_k), тура (8.1.2) санды қатардың мәніне тең s(t_k) үзіліссіз функцияның дискретизациясы болып келеді s'(t),және қайта қалпына келген кезде үзіліссіз функция S'(f) және s'(t) дискретті есептеуге сәйкес S'(f) = S(f) және s'(t) = s(t) Котельников-Шеннон теоремасының жүзеге асуында ғана кепіл болады.

Дискретті түленулер үшін s(kt)  S(nf),және функция, және оның спектрі дискретті және периодты, ал сандық массивтер негізгі периодтардың берілуіне сәйкес Т = Nt ( 0-ден до Т-ға дейін немесе Т/2-ден Т/2-ге дейін), және 2f_N = Nf (f_N-ден f_N –ге дейін), мұнда N – есептеу саны, бұдан:

f = 1/T = 1/(Nt), t = 1/2f_N = 1/(Nf), tf = 1/N, N = 2Tf_N. (8.1.3)

(8.1.3) байланысы динамикалық және жиілікті формадағы дискретті сигналдар ақпаратты шартпен тең бағалылы болып келеді.Басқалай айтқанда: функция есептеудің саны және оның спектрлері ұқсас.Бірақ әрбір комплексті спектрді есептеу екі заттай санды көрсетеді, және соған сәйкес копмлексті спектрді есептеу саны функция есептеуінен 2 есеге үлкен? Ол солай.Бірақ спектр көрінісі комплексті формада – спектральді функцияның математикалық көрінісі,нақты есептеулер екі комплексті есептеудің түйіндестерінің қосылуынан құрылады , ал функция спектрі туралы толық ақпарат комплексті формамен тек бір жағынан тұжырымдалады – шын есептеулер және жалған бөліктің комплексті сандарыныі жиілікті интервалда 0ден f_N –ге дейін,себебі ақпараттың екінші бөлігі 0ден -f_N-ге дейін диапазонда бірінші бөлікпен түйіндес және қосымша ақпаратты жеткізбейді.

Дискретті көрініс кезіндн сигнал аргументі t_k әдетте k сандарымен қойылады (берілгені бойынша t = 1, k = 0,1,…N-1), ал Фурье түрленуі n аргумент бойынша жүзеге асады (жиілікбойынша қадам саны)негізгі периодтарда. N мәні кезінде, 2 еселік:

S(f_n)  S_n = s_k exp(-j2kn/N), n = -N/2,…,0,…,N/2. (8.1.4)

s(t_k)  s_k = (1/N) S_n exp(j2kn/N), k = 0,1,…,N-1. (8.1.5)

Спектрдің негізгі периоды (8.1.4)-те циклдық жиілікте -0,5- ден 0,5 –ке дейін, бұрыштық жиілік -ден ге дейін.Жұп мәнде N шегі негізгі периодты жиілік бойынша ( f_N мәні)жиілік бойынша есептеуде жарты қадамда орналасқан (N/2) және,осыған сай,жоғарғы шектің соммалануы (8.1.5) –те N/2-ге тең болып орналасады.

Еспетеу операцияларында ЭЕМ –да теріс жиілікті аргументтерден басқа (n санынң теріс мәні) және бірдей алгоритмдердің тура және кері Фурье түрленулердің қолданулары 0 -ден 2f_N-ға дейінгі интервалда қабылданады, ал соммалану (8.1.5) –те 0 де N-1-ге дейін сәйкес жүзеге асады.Осыдан ескеру керек ,комплексті түйіндес есптеуде S_n* интервалы(-N,0) екіжақты спектрдің интервалында 0-2f_N S_N+1-n есептеуіне сәйкес (яғни түйіндес есптеулер 0-2f_N инетрвалында S_n және S_N+1-n есептеуі болады ).

Рис. 8.1.1. Дискретный сигнал и модуль его спектра.

Мысалы: На интервале Т= [0,99], N=100 инетрвалында, дискретті сигнал берілген s(k) = (k-i) – тітөртбұрышты импульс k дан 3 -8 ге дейінгі нүктелеріндегі брлік мәнімен. Сигнал формасы және оның спектрінің модулі негізгі жиілкті диапазонда (S(n) = s(k) exp(-j2kn/100 формула бойынша есептеуде) жиілік бойынша қадамда =2/100, 8.1.1 суретте көрсетілген.

Рис. 8.1.2. Модуль спектра. Рис. 8.1.3. Модуль спектра.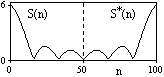

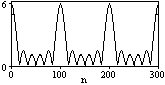
8.1.2 суретінде негізгі спектр дипазонындағы басқа форманың айналдырылған мәні көрсетілген. Формаға тәуелсіз спектр периодты, спектрдің мәнін үлкен интервал аргументі n-ды сол қадамда сақтаған жиілікте анықтаған кезде көз жеткіземіз, как это показано на рис. 8.1.3 суретінде көрсетілген спектрдің мәні айналдырылған.

Рис. 8.1.4. Обратное преобразование Фурье.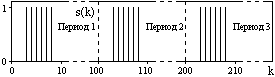

На рис. 8.1.4. суретте дискретті спектр үшін Фурьенің кері түрленуі көрсетілген s'(k) = (1/100) S(n)exp(j2kn/100) формуласы бойынша жүзеге асқан, s(k) функциясының периодтылығын көрсетеін,бірақ негізгі период k={0,99} осы функцияның бастапқы сигналы s(k)-мен толығымен сәйкес.

(8.1.4-8.1.5) түрленулерін Фурьенің дискретті түлнуі дейді (ДПФ). ДПФ үшін негізінде интегралды Фкрье түрленуінің барлық қасиеттері тиесілі,бірақ ескеретін бір жай дискретті функция периодттылғы және спектрі.Екі дискретті функция спектрінің пайда болуы (кез келген операциялардың жүзеге асуындағы сигналдың өңдеуі жиілікті көріністе ,мысалға сигналдардың фильтрациясы жиілікті формада) функцияның периодты сверткасы уақыт көрінісінде сәйкес келеді(немесе керісінше).Осындай свертка циклды деп аталады(8.4 бөлімінде) және оның нәтижесі аяққы бөліктерінде ақпаратты интервалдарды финитті дискретті функциялардың сверткаларынан ажырата алады.

ДПФ өрнегінен әрбір гармоника есептеуінде N операция комплексті көбейтіндісін және соған сай N² операциясының ДПФ толық жүзеге асуын көреміз.Массивтер деректерінің үлкен аумақтары уақыттың заттай шығынына алып келеді.Есептеуді үдету Фурьенің тез түрленуін қолданғанда жүзеге асады.

Фурьенің тез түрленуі (БПФ, fast Fourier transform - FFT).Ол көбейткіштерді(синустар және косинустар) есептегенде базаланады периодты қайталанаты мәндер көп (функцияның периодтылық күшіне байланысты).БПФ алгоритмы қосындыны бірдей көбейтіштермен пирамидалы алгоритммен топтастрады,көбейтіндінің санын қысқартады, қайта есептеуден басқаларын.БПФ-тың тез жүзеге асуы нәтижесінде N стандартты алгоритмнен жүз есе тез жүзеге асады.Осыдан БПФ алгоритмі стандарттыдан да нақтырақ , себебі операция санын қысқарта отырып , домалақтаудағы қателерді қысқартады.

Мысалға,массив саны s_k N = 2^r есептеулеріне ие делік(r - бүтін).Бастапқы массивті екі аралық массивке жұп және тақ есептеулерге бөлеміз:

s_k' = s_2k, s_k" = s_2k+1, 0  k  N/2-1.

Әрбір массивтің ДПФ-ын жүзеге асырайық, функция қадамы 2 –ге тең екекнін ескереміз ( t=1 болса), ал периодтағы аралық спектр N/2 –ге сәйкес тең болады:

s_k'  S_n', s_k"  S_n", 0  n  N/2-1.

Ізделініп жатқан спектрдің S_n бір жартысын алу үшін алынған спектрлерді кешігу теорамасы бойынша спектрларды қосамыз, себебі функция есептеуі s_k" s_k'-ға қатысты дискретизацияның бір қадамына жылжытылды:

S_n = S_n'+S_n"exp(-j2n/N). (8.1.6)

Спектрдің екінші жартысы,біріншімен комплексті түйіндескен, с учетом периода повторения N/2 периодының қайталануына сәйкес аралық спектр келесі өрнекпен анықталады:

S_n+N/2 = S_n'+S_n"exp(-j2n+N/2)/N) = S_n'- S_n"exp(-j2n/N). (8.1.7)

Осы жағдайда көріп отырғанымыздай толық спектрді анықтау үшін N²/4 операциялары қажет аралық спектрлерді анықтау үшін қоса N комплексті көбейтіндісі және қосындысының операциялары қажет, елеулі эффект тудыратын ДПФ –пен салыстырғанда.

Бірақ массивтерді екі бөлікке бөлуде бірінші аралық массивтерге де қолдануға болады, екінші ге де, массивтерде бір ғана есептеу қалғанша жалғаса береді,фурье түрленуі есептеудің өзіне тең.Осыдан түрлену алгоритмі пирамидалы ауыспалы алгоритмге айналады қосылу /айырылумен және бірлік көбейтінді мәнімен exp(-j2n/N) пирамида деңгейімен сәйкес.БПФ-тың бірінші алгоритмі берілген принципте (көп модификациядан,қазіргі уақытта өмір сүретін) Кули-Тьюки-мен 1965 жылы құрастырылған және N/r-ды ДПФ-пен салыстырғанда жылдамдығы жоғарылатты. N көп боған сайын БПФ эффекті де көп.Осыдан N = 1024 болса r = 10-ды аламыз және осыған сәйкес соответственно N/r 100. N = 2^r нүкте санының шартына келсек,ол N_k 2^r нұсқасы ретінде қарастырылады мұнда r – минималды бүтін. N_k < 2^r массивтері 2^r –ге нөлмен толықтырылады,спектр формасы өзгертілмейді. қадамы ғана өзгертіледі спектр көрінісіне қатысты (= 2/2^r < 2/N), сигналдың бірдей көрінісіне қатысты кем болады жиілікті аумақта.Қазіргі уақытта да бар және БПФ алгоритмі басқа негіздемемен және олардың комбинацияларымен, сигналдың нөлдерімен 2^r-ға дейін қосымшаны талап етпейді.

(8.1.7)ге сәйкес есептеулер ,оң жағымен түйіндес негізгі жиілікті диапазон (0, ),(-,0) диапазонына сәйкес емес, ал (,2) диапазонына сәйкес,дискретті деректреде спектрдің периодтылығы,мәнге ие емес,яғни шығыс жиілікті диапазон БПФ-ы (0, 2)-ге тең. Комплексті спектрдің есептеулерінің жалпы саны негізгі диапазонға шартты бастапқы сигналдың нүкте санына тең (нөлдік нүктелерге сай N=2^r-ге қосымша сигналдарға ) Тез кері түрлену алгоритмі (ОБПФ) тура БПФ-тың алгоритміне тең.

БПФ-тың тура және керә алгоритмі қазіргі заманғы  бағдарламалық қамтамасыз етуде анализдеу және цифрлы деректерді өңдеуде кеңінен қолданылады. БПФ жүзеге асыру мысалы 8.1.5 суретінде көрсетілген.

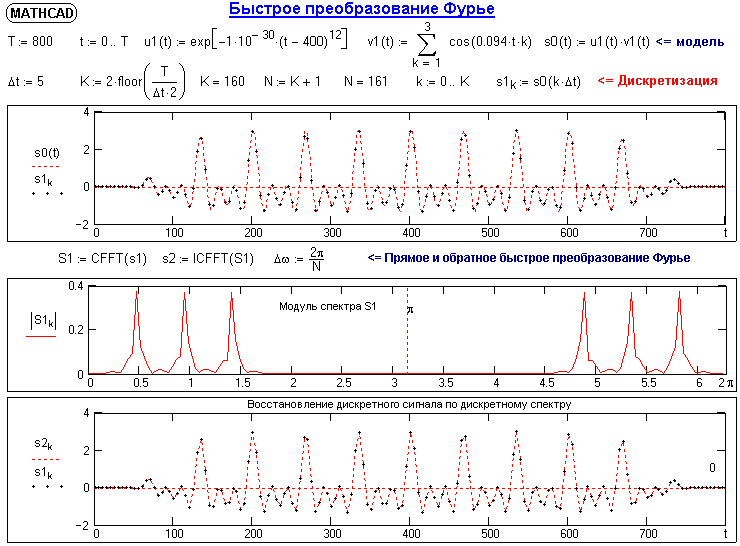
Рис. 8.1.5. Пример БПФ.

ДПФ-ты қолдану. ДПФ-ты қолданудағы негізгі аумақ – физикалық деректердің спектральді анализі.Осыған сай қызығушылықты гармониканың бөлек амплитудасы көрсетеді,оның фазасы емес, және спектр жиіліктен (спектр модулі) амплитудаға қатысты графигі көрсетілген.Көбінде амплитуда шкаласы децибилмен жіктеледі. Децибилдер- амплитудалық мәнге сәйкес логарифмдер. Мысалға , 20 дБ айырмашылығы амплитуданың 10 есе айырмашылығын білдіреді, 40 дБ айырмашылық -100 есеге.Амплитуданы 2 есе айырмашылығы 6 дБ-ге жуық айырмашылыққа ие.Жиілік шкаласы логарифмдік масштабпен жіктеледі.

Спектрді сигналдан есептеу басында, сигнал бөлігі қиылынып алады.Алдын-ала есептеу бөлігінің саны БПФ қолданысында екілік деңгей болуы керек,егер есептеу системасындағы бағдарламалық қамтамасыз етуінде БПФ-тың еркін сандық қатары қабілеттілігі туралы айтылмаған.Кері жағдайда сандық қатар нолдермен толықтырылады керек өлшемге дейін,спектр формасын өзгертпейді және спектр бойынша жиілкті рұқсат беру үлкеюіне қатысады.

Спектрді есептегенде келесі орынсыз эффекті орын алады.Сигнал телімінің Фурье қатарына жіктелуі бір период Т орнын алады,фундаментальді жиілік 1/Т орынының периодты қайталануына байланысты. Осыған байланысты период шегінің функциясы үзіліске немесе кенеттен көтерілуге ие болады, осыдан спектрді бұрмалауы жүзеге асады.Осы эффектті жою үшін салмақты терезелер қолданылады,гауссианға ұқсас,аумағы телім аумағына тең. Анализденген телім салмақты терезелерге көбейтіледі және спектрлердің бұрмалану деңгейінен жойылады.Салмақты терезелер методикасы сигналдарды цифрлі өңдеу курсында қарастыралады.