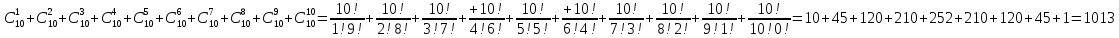- •Институт информационных технологий
- •Контрольная работа
- •Запишите все перестановки из элементов множества {a,b,c}. Найдите к каждой из них обратную.
- •Решите следующие комбинаторные задачи.
- •Определите количество натуральных чисел, не превосходящих 100, которые не делятся ни на 3, ни на 5.
- •11. Постройте для неориентированного графа матрицы смежности и инцидентности, сопряженный (реберный) граф.
Министерство образования Республики Беларусь
Учреждение образования
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»
Институт информационных технологий
Специальность Программное обеспечение информационных технологий
Контрольная работа
По курсу Дискретная математика
Студент-заочник 2 курса
Группы № 781074
ФИО Красносельская Полина Юрьевна
Минск, 2019
-
Даны множества A={1,2,5,8,9}, B={2,7,8}. Найдите их объединение, пересечение, разности и дополнения до множества U={1,2,3,4,5,6,7,8,9,10}.
Объединение:
A B
= {1,2,5,7,8,9}
B
= {1,2,5,7,8,9}
Пересечение:
A B
= {2,8}
B
= {2,8}
Разности:
A-B = {1,5,9}
B-A = {7}
Дополнения до U:
A = {3,4,6,7,10}
B = {1,3,4,5,6,9,10}
-
Даны множества А={a,b,c,d}, B={1,2,3}. Запишите элементы прямого произведения A×B этих множеств. Определите мощности множеств и число их подмножеств.
Прямое произведение:
А×B = {(a,1),(a,2),(a,3),(b,1),(b,2),(b,3),(c,1),(c,2),(c,3),(d,1),(d,2),(d,3)}
Мощности:
А = 4
В = 3
Число подмножеств:
А = 24 = 16
В = 23 = 8
-
Даны множества U={1,2,3,…,100}, M1 – множество всех чисел, кратных 3, M2 – множество всех чисел, кратных 5. Найдите объединение, пересечение, разности и дополнения множеств M1 и M2. Определите мощности множеств.

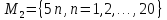
Объединение:
 – множество
всех чисел, кратных 3 или 5
– множество
всех чисел, кратных 3 или 5
Пересечение:
M1 M2
= {15,30,45,60,75,90} – множество всех чисел,
кратных 3 и 5 одновременно
M2
= {15,30,45,60,75,90} – множество всех чисел,
кратных 3 и 5 одновременно
Разность:
M1
– M2
=
 – множество всех чисел, кратных 3, но не
кратных 5
– множество всех чисел, кратных 3, но не
кратных 5
M2 – M1 = {5,10,20,25,35,40,50,55,65,70,80,85,95} – множество всех чисел, кратных 5, но не кратных 3
Дополнения:
M1 = все числа от 1 до 100, которые не делятся на 3
M = все числа от 1 до 100, которые не делятся на 5
Мощности:
M1 = 33
M2 = 20
-
Запишите все перестановки из элементов множества {a,b,c}. Найдите к каждой из них обратную.
{a,b,c} {a,c,b} {b,a,c} {b,c,a} {c,a,b} {c,b,a} - перестановки
{a,b,c} {a,b,c} {a,b,c} {a,b,c} {a,b,c} {a,b,c} - упорядочение
{a,b,c} {a,c,b} {b,a,c} {c,a,b} {b,c,a} {c,b,a} – обратные перестановки
-
Решите следующие комбинаторные задачи.
5.1. Метка состоит из буквы и цифры. Определите количество меток, составленных из 5 букв и 6 цифр.
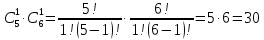
-
В лотерее выбирается шесть разных номеров из первых 45 натуральных чисел. Определите количество возможных вариантов выбора.
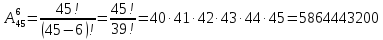
5.3. Определите, сколькими способами в кондитерской можно выбрать 2 булочки из 5 видов, если:
1) нельзя выбирать булочки одного вида, и порядок выбора важен;
2) можно выбирать булочки одного вида, и порядок выбора важен;
3) нельзя выбирать булочки одного вида, и порядок выбора неважен;
4) можно выбирать булочки одного вида, но порядок выбора неважен.
1)

2)

3)

4)
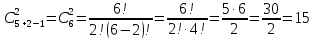
5.4. Из пункта А в пункт B проложено две дороги, из пункта B в пункт C – три, из пункта С в пункт D – четыре, из D в A – пять. Определите, сколько существует вариантов поездок из А в С.
A→B→C: 2∙3=6
A→D→C: 5∙4=20
20 + 6 = 26
5.5. Для записи целого числа используется строка из 16 двоичных цифр. Определите, сколько различных целых чисел может быть использовано при таком способе записи, если первая цифра зарезервирована под знак.
 =
65536 - 1 = 65535
=
65536 - 1 = 65535
5.6. На полке в холодильнике лежат фрукты: 3 банана, 4 груши, 5 яблок. Определите количество вариантов выбора двух фруктов разных видов.
3∙4=12
3∙5=15
4∙5=20
12 + 15 + 20 = 47
5.7. Регистрационный знак легкового автомобиля представляет собой запись двух букв 12-буквенного алфавита и четырех арабских цифр. Определите, сколько различных номеров может быть выдано.

5.8. На каждой из игральных костей может выпасть от одного до шести очков. Определите количество вариантов выпадения очков при подбрасывании трех костей.

5.9. Из колоды в 36 карт произвольно вытягивается 3 карты. Определите количество комбинаций, содержащих ровно 1 туз (напомним, что в колоде 4 туза).
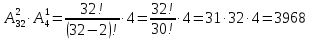
5.10. Для составления пароля, состоящего из трех различных символов, используется 10 цифр. Определите:
1) сколько можно создать разных паролей;
2) сколько можно создать разных паролей, в которые войдут цифры 0 и 1;
3) сколько можно создать паролей, в которых не будет ни цифры 0, ни цифры 1;
4) сколько можно создать паролей, в которых будет или цифра 0, или цифра 1 (но не обе).
-

-
1 цифра – 3 способа (0 или 1, или любая другая)
2 цифра – 2 способа (оставшаяся 0 или 1, или любая другая)
3 цифра – 8 способов (любая другая цифра)
3 ∙ 2 ∙ 8 = 48
-
1 цифра – 8 способов (без 0 и 1)
2 цифра – 7 способов
3 цифра – 6 способов
8 ∙ 7 ∙ 6 = 336
-
1 цифра – 2 способа (0 или 1, или любая другая)
2 цифра – 8 способов (без использованной и оставшейся 0 или 1)
3 цифра – 7 способов
-
∙ 8 ∙ 7 = 112
5.11. Все буквы, составляющие слово «МАТЕМАТИКА», нарисованы на отдельных карточках, которые перевернуты изображением вниз и перемешаны. Определите, сколько существует вариантов собрать это слово «вслепую».
М = 2
А = 3
Т = 2
3!∙2!∙2!=24
5.12. Определите, сколько различных «слов» можно составить из слова «МАТЕМАТИКА».